
University of Amsterdam, Programming Research Group
Kruislaan 403, NL-1098 SJ Amsterdam, The Netherlands
markvdb@wins.uva.nl, alex@wins.uva.nl, x@wins.uva.nl
Mark van den Brand, Alex Sellink,
Chris Verhoef

University of Amsterdam,
Programming Research Group
Kruislaan 403, NL-1098 SJ Amsterdam, The Netherlands
markvdb@wins.uva.nl, alex@wins.uva.nl, x@wins.uva.nl
NOTE! If you are looking for a BNF for COBOL, try the VS COBOL II Grammar
We argue that maintenance and reengineering tools need to have a thorough knowledge of the language that the code is written in. More specifically, for the family of COBOL languages we present a general method to define COBOL dialects that are based on the actual code that has to be reengineered or maintained. Subsequently, we give some typical examples of maintenance and reengineering tools that have been specified on top of such a COBOL grammar in order to show that our approach is useful and leads to accurate and relatively simple maintenance and reengineering tools.
Categories and Subject Description: D.2.6 [Software Engineering]: Programming Environments--Interactive; D.2.7 [Software Engineering]: Distribution and Maintenance--Restructuring; D.2.m [Software Engineering]: Miscellaneous--Rapid prototyping
Additional Key Words and Phrases: Reengineering, System renovation, COBOL
There is a constant need for updating and renovating business-critical software systems for many and diverse reasons: business requirements change, technological infrastructure is modernized, the government changes laws, or the third millennium approaches, to mention a few. So, in the area of software engineering the subject of reengineering becomes more and more important. Reengineering is the analysis and renovation of software, see, for instance, [11] for an introductory paper and [7] for an annotated bibliography on this subject. To aid in the analysis and renovation of software it is crucial to have tool support. We strongly believe that such tools largely benefit from having knowledge of the language they have to analyze or renovate. In other words, tools to aid in reengineering should be based on the grammar of the language they intend to process.
As most of the business-critical software is written in COBOL, we will present a general method describing how to obtain a COBOL grammar, given a number of COBOL programs. Moreover, we explain how to reduce the size of this grammar significantly by means of, as we call it, unification of production rules. Finally, we show that tools that are based on such a compact language definition are useful in reengineering the code written in that language. Thus, the challenge of specifying reengineering tools lies in the (compact) specification of the underlying language. When it comes to defining syntax is is obviously better to use a parser generator, like Lex+Yacc than to write a parser by hand. Therefore, it is not surprising that, e.g., Software Refinery [24], which is based on generic programming language technology incorporates a number of reengineering tools (for more connections between reengineering and generic language technology we refer to [6]).
To emphasize the importance of tools based on language definitions we give a small example. Suppose that we need a tool that analyzes COBOL\ programs by looking for date-related variables and that this tool is solely based on lexical scanning. This implies that the tool will list comments containing the patterns it is looking for, as well. To reduce the number of so-called false-positives it is sensible to modify this tool so that listing of comments will be suppressed. In fact, the tool now contains knowledge of the language it is analyzing. Still many false-positives will be found for various reasons. This can mostly be solved in an ad-hoc manner by adding extra knowledge of the language. This procedure has to be reiterated for a tool that needs to perform another task. In fact, most of the time a tool developer is busy with adding knowledge of the language to the tool instead of implementing the actual reengineering or maintenance task of the tool. So in our opinion it is a better idea to approach this in a more structured manner, by specifying COBOL syntax and subsequently specifying tools on top of that syntax. Which brings us to the matter of defining COBOL syntax. There is a myriad of COBOL dialects. We will discuss in this paper a general method describing how to obtain a practical COBOL grammar that recognizes a particular dialect. Then we discuss how tools can be specified that aid in reengineering and maintenance tasks. At this point the reader may observe that although putting more knowledge in a tool implies less false-positives, the processing overhead will increase. However, since legacy systems are notoriously large, the reduction of false-positives is a serious matter. In the end it pays off to use a tool that has extensive knowledge of the language. Apart from that it can even be the case that a tool that has knowledge of the language improves its performance. For instance, a tool that returns the PROGRAM-ID of a given COBOL program only needs to process the IDENTIFICATION DIVISION whereas a tool that has no knowledge of the language has to process the entire program to find the PROGRAM-ID (if it finds it at all, see Section 5.1 for more details).
Having motivated our work, we will give an impression of it. In Figure 1 we depicted how to obtain a practical grammar that is based on preprocessed code. We briefly discuss the various phases of that process.
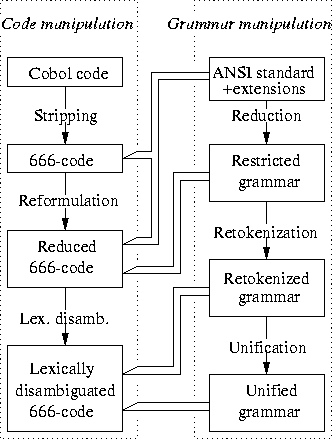
Figure 1: Code and grammar manipulations.
First, we will discuss the left-hand side of Figure 1.
The starting point is COBOL code that needs to be analyzed. In our case
this was a mix of two COBOL dialects provided by a (financial) company.
To be able to analyze and change such code, it is important to minimize
effort. This implies that the code has to be preprocessed. We sketch
this approach: first we strip the COBOL code so that only relevant
columns remain, thus obtaining so-called 666-code . Then we reformulate this
code a bit by performing some global substitutions. For instance, we
substitute THRU for THROUGH. Then we lexically disambiguate
the thus obtained reduced 666-code, for instance, to be able to lexically
distinguish the comment marker * from the multiplication operator
*. The result is lexically disambiguated 666-code.
. Then we reformulate this
code a bit by performing some global substitutions. For instance, we
substitute THRU for THROUGH. Then we lexically disambiguate
the thus obtained reduced 666-code, for instance, to be able to lexically
distinguish the comment marker * from the multiplication operator
*. The result is lexically disambiguated 666-code.
The right-hand side of Figure 1 deals with manipulations on the grammar. The open arrows indicate that the grammar in question understands the code the arrow points at. We have an ANSI COBOL\ grammar at our disposal [22] plus extensions that we found in other sources such as IBM manuals, actual COBOL code, etc. It understands 74, 85, IBM specific code, etc. in 666-form and reduced 666 form. 666-code and reduced 666-code. We reduce the ANSI-grammar plus its extensions by the removal of redundant tokens and we remove all the constructs that do not even occur in the code, for instance, the END PROGAM HEADER did not occur in the code. Thus we obtain a restricted grammar that understands reduced 666-code. Then we retokenize the grammar so that it will recognize the lexically disambiguated 666-code. Finally, we unify the grammar. Roughly, this means that we combine context-free rules into less rules. The advantage of this approach is that the grammar will be reduced in size, which leads to a better performance of the generated parser. Of course, the unified grammar will recognize more programs than the retokenized one, it may even recognize incorrect programs. But since the original code is compilable, this causes no problem (see Section 4.4 for more details).
We emphasize that our approach is not just a reduction of an existing 85 grammar but it uses it as a reference. If constructs that are not present in the standard are located in the code we add those to our grammar. We used iour approach also to define CICS and SQL syntax to deal with embedded calls in COBOL dialects; the only difference is that we have no standard available to save us some work.
In practice, the above code and grammar manipulations will be carried out in parallel. In order to explain our approach we treat those transformations as conceptual entities.
At the time of writing this paper we are in a preliminary phase to design a software renovation factory to restructure legacy code from a large financial company. We are using the methods we report on in this paper to construct a grammar that recognizes their code. In this paper we intend to show that our approach is useful for the construction of tools by giving some examples. In [8] we describe how we can even generate tools for a renovation factory using a grammar as input.
In Section 2 we discuss how to obtain COBOL\ definitions in general. In Section 3 we will elaborately discuss the code manipulation part of Figure 1 where we translate COBOL code into lexically disambiguated 666-code that suits our reengineering purposes. The grammar manipulation part of Figure 1 will be discussed in Section 4. In this section we discuss a general method to define the syntax of COBOL. In section 5, we discuss the specification of tools based on the COBOL syntax definition. In Section 6 we give our conclusions.
In [2] and [3] a formal semantics of a subset of COBOL is presented based on denotational semantics. A reverse engineering tool is based on these ideas which can be used to reverse engineer 74 programs. This tool is based on a COBOL grammar consisting of 170 complex rules in BNF notation, based on this definition the formal semantics of the control statements is defined. These control statements are isolated in a new language MiCo. We give a general method describing how to obtain such grammars, we have specified such grammars, and we specified tools based on such grammars.
In [23] experiences with building a remodularization tool for COBOL using Software Refinery is discussed. We used a system that is similar to theirs to develop tools for COBOL.
In [10] a method is proposed to algebraically specify tools to aid in reengineering and maintenance. Their approach is to base the tools on a database that contains knowledge of the code to be maintained. We stored the knowledge of the code in a language definition of that code. They use traditional parser generation techniques (Lex+Yacc) to generate parsers for specific languages before the actual analysis can take place. In our case we use more sophisticated incremental parser generation techniques. See Section 2 for more comparisons and details.
In this section we will discuss how to define syntax in general and what techniques we used to define COBOL dialects. Then we discuss an ambiguity problem of COBOL that can not be solved easily.
First we enumerate the various COBOL dialects and their compilers.
We note that many COBOL dialects have the possibility to incorporate embedded SQL, JCL, CICS, etc. We can handle those extenstions, as well.
We briefly discuss a number of formalisms in which it is possible to define the syntax of a programming language. They are, EAG [20], Lex+Yacc [16, 21], Refine [24], and ASF+SDF\ [4, 14]. First we will shortly characterize them and then we discuss their merits and shortcomings in the light of defining a COBOL syntax. We refer to the surveys [25] and [27] for a general discussion on the above (and other) formalisms to define the syntax and semantics of programming languages.
Now we discuss relevant properties of the above formalisms in the light of defining COBOL syntax.
Obviously, there is no best formalism to define COBOL syntax. Lex+Yacc\ is proven technology but has as a serious drawback its lack of modularity and its conflicts. Refine which is based on the same parser generation technology also has these problems. On EAGs we can be short. They are not an option since EAGs are not very well supported by tools.
We have chosen for ASF+SDF because we think modularity is essential when describing the syntax of COBOL and its myriad of dialects. Moreover, the ASF+SDF formalism is supported by a programming environment, called the ASF+SDF Meta-Environment [18], which is based on lazy and incremental scanner and parser generation techniques allowing flexible prototyping of language definitions. Moreover, it supports rapid prototyping of tools based on the COBOL syntax, see Section 5 for details.
Another argument in favor of the ASF+SDF Meta-Environment is that it is quite easy to change the context-free grammar rules of company-specific versions of the language, or to define a context-free grammar for languages that resemble COBOL such as Telon [12] (a language used to generate screens of the user-interface of an application). It is also easy to incorporate modules describing CICS and SQL syntax and JCL calls. Since there are many dialects of COBOL and the possibility of embedded calls in them this is a serious argument in favor of ASF+SDF.
Refine and ASF+SDF are comparable: both systems provide facilities for the development of tools to analyze programs. An important difference is that Refine is a commercial product whereas the ASF+SDF Meta-Environment\ is an academic product and can be obtained for free for universities and research institutes. Another difference is that ASF+SDF is based on algebraic specifications whereas Refine has a Lisp-like dialect to write specifications.
To a certain extend it is possible to translate a context-free grammar in SDF to Lex+Yacc. Since SDF permits arbitrary grammars unlike Lex+Yacc this may induce some extra work in manually solving shift-reduce and reduce-reduce conflicts. Furthermore, it is possible to obtain C-code from an ASF+SDF specification. This can be done either automatically or manually, both these approaches are elaborately described in [15]. These possibilities are for us also an argument to work with ASF+SDF.
ASF+SDF is a modular algebraic specification formalism for the definition of syntax and semantics of (programming) languages. It is a combination of two formalisms ASF (Algebraic Specification Formalism [4]), and SDF (Syntax Definition Formalism [13]). The ASF+SDF formalism is supported by an interactive programming environment, the ASF+SDF Meta-environment [18]. This system is called meta-environment because it supports the design and development of programming environments.
ASF is based on the notion of a module consisting of a signature defining the abstract syntax of functions and a set of conditional equations defining their semantics. SDF allows the definition of concrete (i.e. lexical and context-free) syntax. Abstract syntax is automatically derived from the concrete syntax rules.
ASF+SDF has already been used for the formal definition of a variety of (programming) languages and for the specification of software engineering problems in diverse areas. See [5] for details on industrial applications.
ASF+SDF specifications can be executed by interpreting the equations as conditional rewrite rules or by compilation to C. For more information on conditional rewrite systems we refer to [19] and [17]. It is also possible to regard the ASF+SDF specification as a formal specification and to implement the described functionality in some programming language.
There are various forms of ambiguity, many of them are created by associativity and priority conflicts in the context-free syntax rules. Associativity problems can be solved by introducing either brackets in the sentence to be parsed, or by modifying the context-free syntax rules. The associativity problems can be solved in SDF by extending the context-free syntax rules with the appropriate associativity attributes. Priority problems can also be solved by introducing brackets in the input sentence, or by giving an ordening on the context-free syntax rules that cause the priority conflicts.
However, there are ambiguities which are context-dependent. We will give a COBOL specific example: X = Y OR Z (see Figure 2). Depending on the status of Z the root of the parse tree is either = or OR. The program in Figure 2 prints s(success) or f(failure) depending on whether Z is a numeral or a predicate and depending on the values of X, Y, and Z; viz. the results in the table in the program. The conclusion is here that the parse tree depends on the status of Z. Note that the * on line 7 now forces Z to be a predicate but if the * is on line 8 then Z is a numeral.
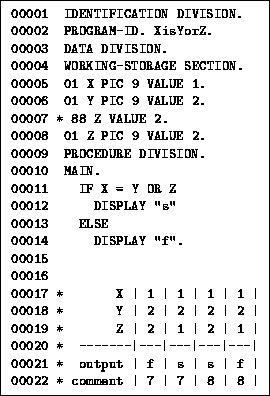
Figure 2: Example COBOL program.
This problem can be solved in SDF by defining a more general context-free syntax rule and by adding an extra pass to adjust the constructed parse tree.
Note that this problem will not occur when we would use EAG because of the facility of semantic-directed parsing. The other approaches that we discussed in Section 2.1 do have this problem, but we think it is harmless since we do not need this type of information in reengineering. At least we did not encounter this problem in real-world code.
As is well-known, COBOL is a huge language. One of the problems in specifying COBOL syntax is that many syntactic variations with exactly the same semantics occur in the language. We also know that the reduction of the size of a COBOL definition leads to better performance, and it makes the specification of tools more easy. So, it is a good idea to preprocess COBOL code by taking away that syntactic freedom that can be dealt with easily in a preprocessor. However, other transformations, like the use of periods instead of scope terminators are not typical preprocessing tasks. For such tasks it is better to specify a tool on top of the COBOL syntax that takes care of such transformations. Usually, such tools will facilitate maintenance and reengineering of COBOL code. For instance, the transformation of implicit to explicit scope terminators (see Section 5.3 for details).
We will devote the rest of this section to a pointwise discussion of a few typical preprocessing tasks.
(>|GREATER) [OR] (=|EQUAL) to >= thus reducing
from eight to one alternative (with (A|B) we mean the choice
between A and B).
Our preprocessor is a one page perl(1) script [26]. Translation of original code to lexically disambiguated 666-code takes about 1 second per 3 KLOC.
In this section we will discuss a general method to obtain a definition of a COBOL syntax that is based on code that has to be maintained or reengineered. As a reference we will work with an as complete as possible COBOL definition in SDF, which is based on the ANSI standard of 85 [1]. This definition contains approximately 1100 production rules but it is still not complete [22]. We will discuss how to obtain the ANSI grammar, and then we discuss how to obtain a specific grammar that recognizes the code that actually has to be maintained or reengineered. This is not necessarily a reduction of the ANSI grammar: constructions that do not occur in it are added to the specific grammar in the same way the ANSI grammar was developped.
The standard way to develop a language definition for an existing language is to base it on an official document containing at least the syntax rules. Developing the definition based on syntax rules results in a parser which accepts only syntactical correct programs. In this section we discuss the syntax definition of 85 based on the ANSI standard [1]. A more detailed description of this process is reported on in [22].
Ideally this process leads to a more or less complete formal definition of the language, however the amount of success depends on the complexity and size of the language. Although 85 is a huge language, a considerable part of the language is defined in [22] along the lines that we discuss below. It consists of about 1100 production rules and it took an undergraduate student four months to specify these rules. As far as we know this is the largest specification of 85. We are aware of [2] and [3] where a tool is described that is based on a COBOL grammar of 170 BNF rules.
Almost all context-free grammar rules of the 85 syntax in [1] are translated into rules in the Syntax Definition Formalism (SDF) [14]. After the definition of a considerable number of rules in SDF, a number of test programs were parsed by the generated parser to test the correctness and completeness of the context-free grammar for ANSI 85. Here we benefited from the advantage of using the ASF+SDF Meta-Environment since it supports incremental parser generation from the context-free grammar.
Next, we describe the problems we encountered during the translation of the context-free grammar rules in [1] into SDF rules. This is a nontrivial process for the following reasons. First of all the size of the ANSI document is huge. But more important is that the ANSI standard is not very well structured. The ANSI document distinguishes the following sets of rules: the so-called general format that gives the formal definition of the syntax, the syntax rules that add properties to the definitions in general format, and the general rules that--they claim--define the semantics. In fact, the syntax definition is scattered over the general format, the syntax rules, and the general rules. The general format is a first order approximation of the actual syntax. The syntax rules and the general rules give more information on the syntax in natural language. For example, the arbitrary order of optional constructs is often defined informally in the syntax rules. The general rules define syntactic constraints, whereas they claim to define semantics. We incorporated all their different syntax descriptions using one formalism: SDF.
In [22] care has been taken of these problems and although the resulting definition is not yet complete it has a (far more) better structure than the ANSI document and is, therefore, useful as an electronic reference manual. In fact, the grammar in [22] could very well serve as the starting point for grammar manipulations as depicted in Figure 1 leading to a more specific grammar that is geared towards recognizing specific COBOL code that has to be analyzed.
To give the reader an idea of the translation process we present an example. We discuss the translation of the PICTURE string environment from the ANSI standard into SDF. Since the complete SDF definition of the PICTURE string environment takes about 90 production rules we confine ourselves to showing how the following rule in general format is translated to SDF rules.
![]()
The intended interpretation of the above rule is as follows. Uppercase words represent keywords, lowercase words represent non-terminals. The curly braces indicate that one of the alternatives has to be chosen. Underlined keywords are obligatory as opposed to not underlined ones.
The translation to SDF rules for this construct is below.
context-free syntax
PIC-LIT OPT-IS PIC-STRING -> PICTURE-DEF
"PICTURE" -> PIC-LIT
"PIC" -> PIC-LIT
-> OPT-IS
"IS" -> OPT-IS
The meaning of the above rules is as follows. We mention that SDF\ is a BNF-like formalism, except that the left- and right-hand sides are switched. The alternatives of a syntax rule are those rules which have the same non-terminal at the right-hand side. PICTURE-DEF, PIC-LIT, OPT-IS, and PIC-STRING are non-terminals, "PICTURE", "PIC", and "IS" are keywords. The first alternative of OPT-IS is an empty alternative.
In the above way the entire translation can be made and a major part of it has been carried out in [22]. The ensueing context-free grammar recognizes 666-code (see Figure 1).
Based on actual code of about 200 COBOL programs, a mixture of OS/VS COBOL and COBOL 370 programs, the SDF definition discussed in the previous section is adapted and reduced to a restricted grammar. The reason that we want a restricted grammar is to improve the performance of the parser generator, the generated parserm and the tools that use the grammar. The performance is not optimal, since he production rules in the ANSI grammar plus extensions have many alternatives (due to the syntactic freedom that COBOL provides), and these alternatives in turn have many members. This implies that the effort to construct the LR-table increases.
First we restrict the grammar by leaving out all those COBOL\ constructions from the ANSI definition that do not occur in the actual COBOL code. Next we carry out a reduction of the ANSI grammar which corresponds with the reformulation phase applied to the code, this yields a restricted grammar. The result is a restricted grammar that understands reduced 666-code.
The next phase in the preprocessing was to lexically disambiguate the reduced 666-code. The reason to do this is not to optimize the performance but to solve some technical problems that deal with ambiguities. Hence, the grammar needs to be retokenized. To give an impression of the retokenization we treat a few typical aspects of it.
In COBOL a period (.) stands for at least three different things: a scope terminator, a DECIMAL POINT, or in a PICTURE it can be a formatting symbol (if DECIMAL POINT is set to COMMA). In order to distinguish a period that terminates a PICTURE we changed other two possibilities into a colon (:). Thus the grammar needs to understand colons.
To distinguish the comment markers * and / from the same tokens for the operations multiply and divide we changed comments into #. Hence, the grammar needs to understand that # indicates layout.
Certain scope delimiters can be dealt with more easily when they are renamed into a single symbol. The reason to do this is purely technical. We changed the scope delimiters == in a COPY statement into @. So the grammar needs to be retokenized in order to understand these symbols.
The grammar manipulations that we discussed thus far share the property that the grammar does not recognize incorrect programs. The restricted grammar can recognize less programs than the ANSI definition and the retokenized grammar parses a lexically disambiguated form of COBOL\ code (which can be seen as a dialect of COBOL). In this section we will discuss a grammar transformation that we call unification. It can parse incorrect programs. At this point we have to make an assumption on the code that we want to analyze: we assume that the code is correct, in the sense that it compiles. Fortunately, our point of departure is COBOL code that is compilable since it is our purpose to maintain or reengineer exactly such COBOL code. The reason that we want to unify the grammar is to further improve the performance of the generated parser and the tools that use the grammar. We emphasize that unification does not imply a reduction of the number of programs that can be parsed, it just means that the grammar is less fine-grained than the original grammar.
Next we will explain what unification is and we give an example of its use. The idea is that we take the least common multiple, to phrase it informally, of all the alternatives of a production rule, thus obtaining a rule that allows possibly more than is permitted by the compiler. Consider the productions:
{A1,...,An} -> A
{B1,...,Bm} -> B
where the set notation {A1,...,An} -> A is used to denote the
set of n productions A1 -> A up to and including
An -> A. The unification of the above rules is
the union of their sets where the output sort is renamed into a
common one:
{A1,...,An,B1,...,Bm} -> C
This operation gives a reduction of the number of production rules if
there is overlap in {A1,...,An} and {B1,...,Bm}. We call
this context-free unification.
Apart from context-free unification we also consider lexical unification. Therefore, consider the following productions:
regexp1 -> C regexp2 -> C
where regexp1 and regexp2 are regular expressions. Their unification is a single production rule
regexp -> C
where regexp is a regular expression that matches when one of the regular expressions regexp1 or regexp2 matches. We call this lexical unification.
The combination of context-free and lexical unification yields a reduction of the number of production rules that is quite dramatical in the case of COBOL. Just as with the ANSI definition we will show how we take care of the PICTURE string environment in the unified grammar. As an indication we give two (simplified) SDF rules originating from the ANSI grammar. They represent the rules for numeric, e.g. 9(6), and alphanumeric, e.g. X(6), pictures:
[9]([1-9][0-9]*) -> PIC-STRING [X]([1-9][0-9]*) -> PIC-STRING
By repeated application of context-free and lexical unification of the rules that define PIC-STRING (approximately 90 in the ANSI grammar) we end up with a single production rule to define the complete PICTURE string in the unified grammar:
[0-9XxAa()pZzVvSszBCRD/,$+\-*:]+ -> PIC-STRING
The above rule expresses that one or more characters that are contained in the text brackets form a PICTURE string, called PIC-STRING. So the above unified rule recognizes that there is a PICTURE string, but not if it is correct. For example, it parses :-) but such a PICTURE string never occurs in compilable COBOL code. In fact, the unified grammar disentangles the structure of the COBOL\ program; which is exactly our intention.
In this way we unified the retokenized COBOL grammar. This resulted in a definition of approximately 300 production rules. It is a month work to obtain this definition. We tested it on a large collection of COBOL\ programs that had to be reengineered (about 200 programs, varying from 20 to 11.000 LOC). The performance of the parser is 130 LOC/sec.
In this section we will explain how to use a COBOL syntax to specify tools that aid in reengineering and maintenance tasks. We specify such tools on top of the COBOL syntax. This is done with the Algebraic Specification Formalism [4] (the ASF part of ASF+SDF). With algebraic equations it is convenient to specify the functional behavior of a tool. The ASF+SDF Meta-Environment supports the rapid prototyping and the development of such a tool. The equations that specify it take as input COBOL code. They perform the specified task by focusing on that part of the code that has to be inspected and/or changed. We will first specify an example tool to make our approach clear and then we discuss some maintenance/reengineering tools. We will provide input/output example fragments to show the functionality of the tools. For more applications of the construction of tools based on grammars we refer to [8] were we generate such tools from a grammar.
We present a simple example to illustrate how to specify tools on top of a COBOL grammar. The task of our example tool pid is to extract from a given COBOL program its PROGRAM-ID. Since the PROGRAM-ID of a COBOL program is located in the IDENTIFICATION DIVISION, we can restrict our tool to only inspect the identification division:
pid(I-div E-div D-div P-div) = pid(I-div)
The variables I-div, E-div, D-div, and P-div stand for the four divisions in COBOL. The above equation expresses that the tool will only focus on the IDENTIFICATION DIVISION. The behavior of pid on that division is described as follows:
pid(IDENTIFICATION DIVISION.
PROGRAM-ID. Id.
Author Inst Wdate Cdate Remarks) = Id
The variables Id, Author, Inst, Wdate, Cdate, and Remarks stand for the possible fields in the identification division. This last equation expresses that for a given IDENTIFICATION DIVISION the pid tool returns the variable Id which is the PROGRAM-ID.

Figure 3: Cryptic example program.
This trivially specified tool is capable of extracting the correct PROGRAM-ID in the cryptic COBOL program of Figure 3. The program compiles with the Microfocus COBOL compiler. Of course, it is an artificial program, but it shows that even though the keyword PROGRAM-ID does not appear literally in it, our simple tool extracts the name: Pid-Bull. This is due to the fact that the tool has knowledge of the language the program is written in. Needless to say that with grep-like tools the correct PROGRAM-ID would never have been found.
Now that we have an idea of how to conveniently specify tools, we will discuss some tools that have been specified to aid in maintenance and reengineering. We describe them briefly and provide examples of their input/output behavior to illustrate their functionality and power.
In COBOL we can distinguish so-called in-line and
out-of-line PERFORM statements. An in-line PERFORM is an
iterative construct that is comparable to, for instance, while-loops in
PASCAL. An out-of-line PERFORM is actually a procedure call. The
out2in tool transforms an out-of-line PERFORM to an in-line one.
This is useful since for most analysis tools it is often convenient that
the physical order of the code equals the execution order. Of course,
it is possible to re-implement this functionality in every tool again,
but it is, in our opinion, a better idea to make a tool that performs
this task, so other tools can use this tool if necessary.

Figure 4: Out-of-line to in-line transformation.
In Figure 4 an example fragment and its transformed output
are shown. We can see that the out-of-line construction at the left-hand
side is replaced by the contents of the called paragraph ![]() resulting in an in-line construction. Note that the contents of an
in-line PERFORM may only contain statements, so it is not a simple
textual replacement, hence the omission of the periods after
resulting in an in-line construction. Note that the contents of an
in-line PERFORM may only contain statements, so it is not a simple
textual replacement, hence the omission of the periods after ![]() and
and ![]() in the in-line version. In fact, the out2in\
tool also flattens the code that the out-of-line PERFORM calls.
The straightforward specification of the out2in tool consists of
about 25 ASF equations.
in the in-line version. In fact, the out2in\
tool also flattens the code that the out-of-line PERFORM calls.
The straightforward specification of the out2in tool consists of
about 25 ASF equations.
In 74 there is no explicit scope terminator for IF statements. All (open) IF statements are closed by a period. Furthermore, an ELSE can be closed by another ELSE that is matching a ``higher'' IF. In 85 an explicit scope terminator END-IF has been added as an optional feature. The Add-END-IF tool (aei for short) transforms the implicit scope terminators into explicit ones. In Figure 5 we give an example fragment and its output.

Figure 5: Add END-IF transformation.
It will be clear that the insertion of explicit scope terminators improves the legibility of the code. So, this tool aids in reengineering and maintenance. In practice, such transformations are part of migrations from 74 to 85 code. The specification of this tool comprises about 25 equations. We note that tools for the insertion of other scope terminators, like END-READ or END-WRITE, can be specified in a similar way.
We observed that when others work with our grammar to specify tools, they need more time to develop them. This is due to the fact that they did not know all the intricacies of the grammar. After exaplanation of difficult COBOL contructs the development time decreased.
One of the advantages of using the ASF+SDF Meta-Environment is that given an SDF\ definition of COBOL it is possible to generate tools for COBOL programs. We already saw the incremental generation of parsers during the development of a COBOL grammar. An elaborate discussion on the subject of generating such tools is out of scope. See [8] for details on how to generate tools for reengineering purposes using a context-free grammar as input. We mention here that the development of unparsers is supported by an unparser generator tool [9], since unparsers aid in reengineering and maintenance. The unparser generator generates a set of equations which can be fine-tuned in order to obtain the desired layout of COBOL programs. The equations translate a COBOL program to a language independent expression that can be translated to ASCII-text or TeX-code. The TeX output can be used to produce correct documentation generated directly from the code. In Figure 6 we have extracted the PROCEDURE DIVISION of the program in Figure 2 to give the reader an idea of the functionality of our COBOL formatter.

Figure 6: Typesetted fragment of a COBOL program.
The purpose of an unparser is not only to improve the readability of code, but it can also be of use when migrating from one compiler to another. The Microfocus compiler does not mind when, for instance, PROGRAM-ID does not start in the A-area, but another compiler might (see the program in Figure 3). Then an unparser is useful to modify existing code to meet the standards of the new compiler. Another application of an unparser is that code can be made migration-ripe by uniformizing it so that certain assumptions on the form of the code can be made in order to facilitate massive automatic migrations.
The generation and fine-tuning of an unparser for COBOL given the grammar we discussed in Section 4.4 was less than one week work. This is due to the fact that although for each production rule equations are generated, half of them need small modifications, since it is impossible to predict, in general, how an arbitrary language has to be formatted.
In this paper we have motivated that in order to specify reengineering and maintenance tools for COBOL it is convenient that such tools are built on top of a COBOL definition that is geared towards the specific COBOL code that has to be processed by such tools. We have shown that it is sensible to separate the development of the tools from the development of the grammar that the tools use. To aid in the development of the grammars, we have presented a general method to specify COBOL\ that uses on the one hand an ANSI 85 grammar plus extensions that we found in IBM manuals, and on the other hand real code that has to be reengineered or maintained. Since there are many COBOL dialects such general methods are useful in the development of tools for COBOL. It turned out that specifying tools on top of such grammars is now a convenient task. In fact, in [8] we show that tools can now be generated from the grammar.
We used modular techniques to specify the grammars and the tools. This guarantees that (parts of) grammars and tools can be reused without problems since those techniques support definition of arbitrary context-free grammars. So we do not have the traditional shift-reduce and reduce-reduce conflicts that come with Lex+Yacc-like formalisms.
Concluding, we hope to have shown that the quality of reengineering and maintenance tools drastically improves when these tools are based on a unified context-free grammar of the language in which the code has been written.