![[*]](http://www.wins.uva.nl/pict/latex2html/foot_motif.gif)
Programming Research Group, University of Amsterdam
Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
markvdb@wins.uva.nl, alex@wins.uva.nl, x@wins.uva.nl
Mark van den Brand, Alex Sellink,
Chris Verhoef
![[*]](http://www.wins.uva.nl/pict/latex2html/foot_motif.gif)
Programming Research Group,
University of Amsterdam
Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
markvdb@wins.uva.nl, alex@wins.uva.nl, x@wins.uva.nl
We present an approach for the generation of components for a software renovation factory. These components are generated from a context-free grammar definition that recognizes the code that has to be renovated. We generate analysis and transformation components that can be instantiated with a specific transformation or analysis task. We apply our approach to COBOL and we discuss the construction of realistic software renovation components using our approach.
Categories and Subject Description:
D.2.6 [Software Engineering]: Programming Environments--Interactive;
D.2.7 [Software Engineering]: Distribution and Maintenance--Restructuring;
D.2.m [Software Engineering]: Miscellaneous--Rapid prototyping
Additional Key Words and Phrases:
Reengineering, System renovation, Restructuring, Language migration, Software
renovation factory, COBOL
Software engineers are faced with serious problems when dealing with the renovation of large amounts of legacy code. Manual approaches are not feasible, in general, due to the amount of code. This makes renovation by hand unreliable if not impossible. In [43,54] we can read that two key factors drive the decision to use an external, mass-change factory. The first factor is the number of lines of code to alter. If this number exceeds two million most in-house workbenches cannot handle this and a factory must be used [43,54]. The second factor is whether there are reasonable standards for manipulation or analysis that lend themselves to rules-based modification, or identification. Nowadays, it is more and more recognized that a factory-like approach to renovate legacy code is a sensible paradigm. In [43,54] a factory is a set of tools that are owned and operated by a vendor. The vendor's employees operate the technology, either by setting up the factory on-site or at a central facility. For instance in case of Year 2000 remediation, exponents of such factories are the tools that Reasoning produces [81] and the tools that the Emendo Software Group produces [35]. Emendo was selected in 1997 and 1998 by the Gartner Group [43,54] as technology leader. Capers Jones, probably the most frequently quoted researcher on software productivity statistics, suggests not just that software renovation factories for Year 2000 remediation should be used, he even proposes the use of a global network of Year 2000 repair factories, with three (or more) Year 2000 facilities located eight time zones apart so that Year 2000 repairs can proceed on a 24-hour-a-day basis [53, loc. cit. pp. 89, 115, and 182].
In our opinion, it is relevant to investigate how software renovation factories can be constructed, in general. In this paper we discuss the generation of major parts of typical components. These components should preferably be reliable, maintainable, reusable and thus compositional, and easy to construct. Moreover, the components should be dialect proof. Components should also be able to handle programs containing mixed languages. From [53] we can learn that about 30 percent of the US Software applications contain at least two languages. In that case many Year 2000 search engines come to a halt [53]. In [53] the combination of COBOL and SQL is mentioned as a common combination. We applied the component-generation technology (outside this paper) to mixed-language applications like COBOL and SQL and/or CICS (see Section 1.1 for details).
In our opinion, there is a need for a construction methodology for components to be used in software renovation factories. In this paper we propose a method to generate substantial parts of such components from a context-free grammar. Such a grammar recognizes the code that has to be renovated. In general, it takes an effort to obtain such a grammar. In [15] a method is discussed to obtain grammars from legacy code. Fortunately, in some cases computer aided support to generate grammars can be used [90,94]. We will show in the present paper that due to our generic approach and the presence of a grammar, the components we develop are reliable, maintainable, maximally reusable, and their implementation is usually measured in minutes.
In Section 2 we give our viewpoint on what a software renovation factory is. In Section 3 we discuss in detail what implementation platform we use, and we discuss related implementation platforms that could serve the purpose of generating transformations and analysers as well. In Section 4 we explain how we generate transformations and analysers in principle. In Section 5 we give an elaborate example of how to instantiate generic analysers and generic transformations generated from a given simple grammar. In Section 6 we elaborately show how to reuse existing components. In particular, we reuse the components that we defined in Section 5 for a dialect that we defined in Section 6. In Section 7 we show that our approach is robust. We define yet another dialect of the language we use in Section 5. Then in Section 8 we will apply our approach to COBOL in order to show that the technology that we propose scales to real-world grammars (and realistic problems). Finally, in Section 9 we draw some conclusions.
In [44] we can find a control-flow normalization tool for COBOL74 developed using the TAMPR system [10] - this is a general purpose program transformation system. With the use of REFINE [81] it is also possible to develop components for software renovation. With the TXL transformation system [22] it is also possible to construct software renovation components. All these systems share the property that the transformations are entirely coded by hand. We propose a method to generate substantial parts of them from a given context-free grammar. One of the benefits of our approach is that we can reuse components for different dialects whereas in the above cases the components have to be rewritten.
In attribute grammars [1] an implicit tree traversal function is present. It is comparable to our generated traversal functions. Since they are implicit, it is not possible to manipulate syntax trees so it is difficult to express program transformations using that technology. Higher order attribute grammars [103] is an extended form of attribute grammars in which the traversal functions are no longer implicit. In principle, we think that it should be possible to implement our generic approach using higher order grammars. We have not seen any publication that discusses the generic construction of components using attribute grammars.
In the thesis of Tip [99], the generation of program analysis tools is discussed. The emphasis is on the generation of tools for source-level debugging [98] and for computing various types of program slices [100].
In [29], an application generator called GENOA (Generator of Analyzers) is presented which is a generator of analyzers (it has been applied in [30] in order to build an application generator for the easy specification of testing and analysis tools). The accompanying language, also called GENOA, works directly on a certain parse tree data structure for which useful operations are defined within the language. In this way, it is easy to define analysers. In order to have access to the GENOA data structure, there is a system GENII with accompanying language GENII (GENOA Interface Implementation) that maps the output of an arbitrary parser to the data structure used by the GENOA system. In this way, it is possible to define generic analysers independent of the language. When the language changes, it is only necessary to change the GENII specification. In this paper, we propose an alternative solution for dealing with dialects. We do not need to make changes, in general, to the tools at all. We modify the grammar. GENOA is a domain specific language; the word Generator refers to the fact that from a GENOA specification of an analysis tool you can generate its implementation. We generate the specification of analysis and transformation components from the specification of the language for which the tools are intended. As with GENOA, in our case, it is simple to implement analysis and transformation tools. One of the merits of using GENOA is that it is a framework intended for reusing existing parsers successfully. From [85], we know that reuse is a far from trivial task. A crucial limitation of the GENOA system, is that all accesses of the parsed code are read-only. Therefore, it is not possible, as in our case and in the case of REFINE, to implement transformations. We have to implement parsers ourselves. This takes time and effort, but using sophisticated technology, this is not too much of a problem (see [17,90,94] for more information). An advantage of having the grammar, is that we can gear the grammar towards reengineering, which is not possible when reusing a parser.
In [78], requirements for advanced Year 2000 maintenance tools are discussed. Remediation is done using a so-called correction assistant. This assistant automatically generates a transformation which transforms any statement into itself, but it does not transform larger structures. From an arbitrary context-free grammar, we generate all the necessary traversal functionality that enables arbitrary identity transformations. Moreover, we generate similar functionality for analysis components, and we are able to combine both: an analysis component can serve as a condition for a transformation. Also in [78] a generation assistant under development is mentioned. It is capable of handling larger syntactic structures than on the statement level. In our approach, this is already possible for both transformation and analysis functionality.
We use a generic interactive programming environment for our implementation purposes. We discuss related implementation environments, like REFINE, in Section 3.3.
We see a factory as a set of assembly lines, an assembly line consists of a number of consecutive components. The components themselves are implementations of conditional term rewriting systems with possibly negative premises [60,37]. To understand the contents of this paper is it not necessary to understand the mathematical details of conditional term rewriting with negative premises. We refer to [37] for a formal treatment of these issues. In this paper it suffices to have an an intuition of what a factory is.
The purpose of a software renovation factory is to handle the transformation of massive amounts of code (see Figure 1). First, the code is translated by a parser into an annotated abstract syntax tree. Then the annotated abstract syntax tree is manipulated, e.g., transformed or restructured, according to the desired renovation strategy. Finally, an unparser translates the abstract syntax tree back to text. So, parsers, analyzers, transformations, and unparsers are components of a software renovation factory. Parsing and unparsing components can be obtained by powerful techniques: they can be generated from the context-free grammar of the language to be parsed or unparsed. Lex and Yacc [52,71] are well-known examples of a scanner generator and an LALR(1) parser generator, respectively. We use more sophisticated technology to generate parsers. See [17] for an overview of current parsing technology in reengineering and a comparison with the techniques that we use. For the generation of unparsers from a context-free grammar we refer to [18]. The primary focus of this paper is to show that it is also possible to generate other components of a software renovation factory that are easy to implement, reusable, and robust. They are the components that are part of assembly lines in a software renovation factory.
If we zoom in on the middle part of Figure 1 we end up in Figure 2. On the parse tree level of the software renovation factory, we can discriminate three phases. First the code needs to be pretreated. We call this the preprocessing phase. A very common example is to uniformize code, but many more preprocessing operations can be thought of. The uniformization of code is also a first step in Sneed's reengineering workbench [97]. Normally, we pretreat the code in order to be able to perform the main task as smooth as possible. Then we enter the main processing phase. Usually, it is necessary to shape up the code after the main operation. We call that postprocessing. All our examples of assembly lines exhibited these three phases. Fortunately, many pre- and postprocessing steps can be reused over and over again. Most notably, uniformization of code, but there are many more examples. In each phase we can combine components. In some cases, the order of components is irrelevant. In Figure 2, such components are enclosed in dotted rectangles. The fixed ordering of a number of components is called an assembly line. Although we have three phases in a factory the assembly lines can consist of many more components than just three as suggested by Figure 2.
ASF is based on the notion of a module consisting of a signature defining the abstract syntax of functions and a set of conditional equations defining their semantics. SDF allows the definition of concrete (i.e., lexical and context-free) syntax. Abstract syntax is automatically derived from the concrete syntax rules.
ASF+SDF has been used for the formal definition of a variety of (programming) languages and for the specification of software engineering problems in diverse areas. See [12,13] for details on industrial applications.
ASF+SDF specifications can be executed by interpreting the equations as conditional rewrite rules or by compilation to C [61]. For more information on conditional rewrite systems we refer to [66] and [58]. The conditional rewrite rules may also contain negative conditions. See [60] and [37] for more information on the semantics of such systems. It is also possible to regard the ASF+SDF specification as a formal specification and to implement the described functionality in some programming language by hand.
The generic components that we discuss in this paper are generated ASF+SDF modules. Since we use Generalized LR parsing [70,101,82,102] it is possible to combine grammars without losing the property that we can generate a parser for them (the advantages of using Generalized LR parsing are discussed in detail in [17]). This implies that our grammars are modular. The modular structure of the underlying context-free grammar is clearly visible in the generated components. Each module in the context-free grammar corresponds with a module in the generated components. Each context-free grammar rule corresponds with an equation in a generic component. We generate so-called default equations. A default equation is applied when none of the other equations can be applied successfully. So in our case the system will use the generated equations by default, and hand-written equations whenever they are applicable.
In Figure 3 we show a very simple module defining the
LAYOUT for a certain language. In this module we see an
exports section. SDF has three types of sections: exports,
imports and hiddens sections. In Figure 3, we only
see an exports section. It contains lexical syntax only.
It describes that terms (think of terms as source code fragments)
of the (predefined) sort name LAYOUT consist of two percent signs
followed by anything not being a return, zero or more times, followed
by a newline (denoted \n). Similarly, the second rule states
that a space or a tab or a newline is LAYOUT.
In Figure 4 we display the syntax for a simple language
defining the syntax for some dialect of Booleans. We depicted it
to explain SDF in more detail. First we see that it imports the
Layout module. An imports section can only contain a list of
module names. An exports and hiddens section can contain
various paragraphs. Both sections may contain sorts paragraphs
containing a list of sort names. An example is sort name BOOL
in the sorts paragraph. Both may contain lexical syntax
paragraphs (like we saw in Figure 3). Both sections may also
contain context-free syntax paragraphs. Figure 4 defines
Tony Hoare's symmetric syntax for conditionals using two triangles.
It defines the literals True and False, the Boolean
connectors disjunction, denoted |, and conjunction (&).
The attribute {assoc} states that these operators are associative.
The negation is defined using a tilde-sign (~). Then the syntax of
Tony's conditional operator is defined. Furthermore, we allow brackets
in Booleans. The attribute {bracket} indicates that the
parentheses are not stored in the abstract syntax tree. This means
that expressions that are equal upon parenthesis are considered equal
during computations. Both sections may also contain a variables
paragraph. We can declare variables of any type that we need later on
to define the semantics of our syntax. In Figure 4 we specify
that Bool1, Bool23, and Bool' and such may occur as
variables of type BOOL. Finally, both sections may contain a
priorities paragraph. We see an example of this in the exports
section of the Booleans module. It expresses that the &
binds stronger than the |.
![]()
For a general reference to term rewriting we refer to [66]. For more information on conditional term rewriting we refer to [58] and to [59,57,105,106] for implementations of conditional rewriting. We refer to [60] and [37] for details on conditional rewriting with negative premises. We give an example of the above notations in ASF.
In Figure 6 we present a tool [90,94] from our
CALE factory (CALE stands for Computer Aided Language Engineering). It
sorts BNF rules with respect to left-hand sides. We show this component
in order to explain the full syntax of ASF (for more information on CALE
tools we refer to [90,94]). We already saw that each rule
has a tag. Tags divide equations into two different classes. If the
tag starts with "default-" it is a so-called default equation.
In all other cases it is a non-default equation. Default equations are
applied only if all non-default equations fail. (Within one class the
choice between applicable equations is random.) We will use default
equations in the generation process later on. A conditional rule can be
defined using the double line. Negation is denoted in a C-like fashion
(!=). Below the double line we also see user-defined syntax,
like with the Booleans. Important is that it is of the form s=t like
in the above mathematical formula. For a more elaborate treatment of
the ASF formalism we refer to [8] and [25].
True & True | True understands the structure of the
Booleans. Note that the window is a generated structured editor
[67]. The text structure is visualised by the so-called focus.
In the example above the focus shows that the & binds stronger
than |. We pushed the Reduce button and in the lower
right window we see that the result is rewritten to True. On the
background we see the module containing the syntax and semantics of the
Booleans. This module is used to reduce the Boolean expression.
For more information on the ASF+SDF Meta-Environment we refer to [63,64].
In Figure 9, the buttons at the left of each window are implemented using SEAL. The front window is an editor that understands SEAL. If we press the Typecheck button, it checks for type errors in the SEAL script. If we press the CompileAndLoad button, LeLisp [50] source is generated that is runtime linked to the ASF+SDF Meta-Environment, which results in the addition of buttons with the specified behaviour to the window on the background. In this way we can runtime add or remove buttons or we can modify their functionality. Part of the coordination script can be seen in the front window: it describes the functionality of some Aeqs button (we will explain these buttons later on). This part of the SEAL-script describes that we combined some components. Using this approach we can effortlessly reuse components over and over again. See [69] for a reference to SEAL and see [65] for a more elaborate discussion of component-based software engineering in general.
We recall that the Centaur system is used as the implementation platform for the ASF+SDF Meta-Environment. In [24] we can read that the rivalry between the metalanguages ASF+SDF and Metal/Typol has been a fruitful source of inspiration for the development of the ASF+SDF Meta-Environment. Needless to say that both systems are strongly related. An important difference between the two approaches is that in the ASF+SDF Meta-Environment the abstract syntax is automatically derived from the concrete syntax and vice versa. In the case of Metal/Typol the form of the abstract syntax tree has to be defined by hand, so the unparsing cannot be generated, but needs to be specified by hand. A language called PPML [77] is used for that purpose.
In [19] a tool for building application generators called Stage is discussed. In [20] this is extended with the tools PG2 and WOODS . This effort has lead to a commercially available tool for building application generators discussed in [95] that is called Metatool . This tool is used in [29] to construct the GENOA/GENII system.
There are many more systems being reported on in the literature with the same goal as the ASF+SDF Meta-Environment: generation of interactive programming environments. We mention some of them but we will not treat them here. We mention the PSG system that produces interactive, language-specific programming environments from formal language definitions [4]. The Gandalf system enables the semi-automatically generation of programming environments [42]. The Pan Language-based editing and browsing system is a multi-language window-based editing system that is fully customizable and extensible [5]. Then we have the compiler construction system Eli, which is an open system where it is easy to add tools or replace them; everything controlled by an expert system [41]. There is the language development laboratory whose main components are a tool for language design based on a component library and a knowledge-base plus a test set generator for the generation of program examples to test the defined language [86]. In [36] IPSEN, Integrated Project Support Environment, is discussed. It uses PROGRESS, a formal language to based on graph rewriting [87].
One of the authors (G.B. Kotik) is currently with Reasoning Systems, a company founded in 1984 in order to apply the body of basic research in knowledge-based programming to commercial problems. Reasoning develops special purpose knowledge based program generators and programming environments for various domains. Promising applications are in fields where highly reusable specifications can be built, where there is a great utility in developing and prototyping formal very-high level specifications.
Obviously, we are dealing with a system that is related to the many systems that we just discussed, including the ASF+SDF Meta-Environment. While Software Refinery is developed in a commercial environment from the beginning, the development of the ASF+SDF Meta-Environment has been been developed in an academic environment. The official beginning forms a European project called Generation of Interactive Programming Environments. Let us quote from the ESPRIT 1985 Status Report [46], where the objectives are stated (this can be considered the first publication discussing the ASF+SDF Meta-Environment).
The main objective of this project is to investigate the possibilities of automatically generating interactive programming environments from language specifications. An interactive programming environment is here understood as a set of integrated tools for the incremental creation, manipulation, transformation and compilation of structured, formalized, objects such as programs in a programming language, specifications in a specification language, or formalized technical documents. Such an interactive environment will be generated from a complete syntactic and semantic characterization of the formal language to be used. In the proposed project, a prototype system will be designed and implemented that can manipulate large formally described objects (these descriptions may even use combinations of different formalisms), incrementally maintain their consistency, and compile these descriptions into executable programs.
Both systems are based on dialects of Lisp. Both systems have their roots in the late seventies/early eighties. Both systems build abstract syntax trees in detail. Both systems have a way to vizualize the syntactic structure in an editor. Software Refinery uses hyperlinks and the ASF+SDF Meta-Environment uses a generic structured editor. But see [40,94] for HTML support for the ASF+SDF Meta-Environment. Both systems allow the use of concrete syntax of the parsed language in the description of the behaviour of tools. In Software Refinery this is a little less smooth, but its there. Both supporting formalisms REFINE and ASF+SDF deal on an abstract level with translations and transformations. REFINE is based on set theory, combines both declarative and imperative programming paradigms, includes transformation rules, syntax-directed pattern matching, has higher-orderness, and has traversals in the language. ASF is algebraic and higher-orderness is not incorporated. Both languages are relatively extensive. Some notions are more convenient in ASF and others are more convenient in REFINE. Apart from that the languages are comparable. A difference is the user-definable syntax of ASF (by SDF). In the ASF+SDF Meta-Environment we generate similar traversals to those in Software Refinery (see this paper). Both systems allow escapes to the underlying Lisp system. This is more frequently found in software Refinery than in the ASF+SDF Meta-Environment. A difference is the use of parser technology. Refine/Dialect [79] uses mainly LALR(1) parser generation technology whereas the ASF+SDF Meta-Environment uses generalized LR parser generation technology [70,101,82,102]. Reasoning is implementing generalized LR parsing as well. Software Refinery has error recovery and the ASF+SDF Meta-Environment does not have that. See [17] for an elaborate treatment of parser technology and reengineering. Reasoning has the Refine/Intervista windowing toolkit to construct GUIs [80]. The ASF+SDF Meta-Environment uses SEAL [68]. Refine/Intervista is low-level compared to SEAL.
In fact, it is hard to find anything that can be done using REFINE that cannot be done with the ASF+SDF Meta-Environment, and vice versa. A major advantage of REFINE for companies that there is a company behind it and a major advantage for the research community is that behind ASF+SDF Meta-Environment there is a research community (for instance, the source code is available).
We discuss the various ways of constructing components for a software renovation factory. Given a specific renovation problem in a specific language for which a component has to be developed, several approaches are possible to construct the component. We introduce the following abbreviations LP, LS, PP, and PS standing for language parameterized, language specific, problem parameterized, and problem specific, respectively. They all lead to a tool, see Figure 10. The classical way of constructing a component for a given problem in a given language is handcrafted construction of the component, that is, the LS-PS approach. A serious problem in renovation is that every new customer uses a new dialect so the component has to be re-implemented. A more generic approach can solve that problem. Known generic examples are LP-PS components: parser generators [52,71] and unparser generators [18], which take the language as a parameter. Examples of LP-PP components are generic component generators that can be instantiated with a specific problem in a specific language to obtain a component solving the specific problem.
The LP-PP approach to construct a component is depicted in Figure 11. In this figure we assume the presence of input code in some input language and some given reengineering problem, for instance, an analysis or a transformation task. The figure describes a method to obtain components to perform the reengineering task. First we use a generator that takes the grammar parameter as input. This generator generates a generic component that can be instantiated with the specific problem thus obtaining the component that we need to solve the given problem. We have four grammars: one that recognizes the input code, one that recognizes the output code, one that recognizes both, and one that recognizes the results of an analysis. Recognition of code is expressed with the asymmetric open arrows. In our approach, a component that transforms input code into output code should understand both grammars, in order to be able to combine transformation components sequentially. This is expressed in Figure 11 by the merge operator. Note that the implementation should be able to merge grammars in a convenient way without having reduce/reduce and shift/reduce conflicts, so Lex+Yacc approaches are not always satisfactory (see [72] for a textbook on Lex+Yacc and chapter 8 for an elaborate treatment of shift/reduce and reduce/reduce conflicts and how to solve them). We do not have these problems, since we use generalized LR parsing which handle arbitrary context-free grammars (see [17] for more information). Thus, we obtain a merged grammar: the I/O grammar that understands both the input and output code. Given this merged grammar a generator generates a generic code transformer.
A component that performs an analysis should have knowledge of the input code and the types in which the data is presented, for instance, a Boolean value or a (natural) number. So, the analyzer generator takes as arguments the input grammar and the result data type to generate the generic analysis functions. Now we come to the PP part: for a specific reengineering task, say a transformation or an analysis, we can instantiate the generic components to obtain a specific component that implements the reengineering task. This instantiation consists of writing the non-predictable parts of the component. In this way we can generate the various components that are necessary in a software renovation factory.
Next, we will explain how the generation process works by giving a very simple example and the output of the generation process. To that end we use the grammar of Figure 12. It is a very simple grammar, and it does not mean anything in particular. We present our development environment for software renovation factories only to illustrate the generation processes.
The symbols U, V, and W are nonterminals. In practical cases they could be Declaration, Statement, or Program. In SDF we declare them in a sorts paragraph. In fact, we can generate this sorts paragraph, using the button AddSorts. The quoted symbols K, L, and M are literals or keywords. Practical examples of keywords are begin, end, if or a semi-colon. This example grammar uses SDF syntax. For the sake of comparison, in BNF-style the rule is denoted as:
<W> ::= K <U> L <V> M ;
The generation process consists of two parts: a part that creates new syntax, which is a transformation from SDF to SDF, and a part that creates new behaviour, or semantics for the new syntax. The latter is a transformation from SDF to ASF. We have this situation twice: for generic transformations and for generic analyzers. So we end up with four buttons: Tsyn, Teqs, Asyn, and Aeqs. We will show the output of the components attached to these buttons and explain the generated code. We use this process to generate for a given grammar the traversal and analysis syntax and semantics. In the next paragraphs we give a short characterization of the generated output of the example grammar (Figure 12).
We import a module called TA-basis. In the language independent
module TA-basis some basic issues are handled. Part of the module
TA-basis is depicted in Figure 14. In Figure 14,
we omitted those parts that are not relevant for the purpose of this
paper (denoted as [..]). Next, we export a context-free syntax
rule for each sort of the grammar (U, V and W in
the example). This syntax is used to express that some tool is applied
to some code fragment. If u is a code fragment of sort U,
then t_U(u)^{ } denotes that tool t is applied to u.
How to compute the result is explained in a moment (Figure 15).
In Figure 14 we see that TRANSFORM and ANALYSE are nonterminals as well. We recall that in SDF it is possible to define variables for each nonterminal. This is done for the sorts TRANSFORM and ANALYSE in the variables paragraph in Figure 14. This enables us to reason about arbitrary terms (functionals) of sort TRANSFORM or ANALYSE. In Wile's calculus of abstract syntax trees [109], these functionals are called catamorphisms. An example of a function name is: ADD-END-IF_Sentence. The terminal ADD-END-IF is defined by an operator in a factory to be of sort TRANSFORM. On the level of COBOL sentences we have generated the syntax
TRANSFORM "_Sentence" "(" Sentence ")^{" Attr-s "}" -> Sentence
This syntax can immediately be used by the operator and the bookkeeping on defining it has been done automatically. The Attr-s is a sort that can be used to put attributes in. This can be anything, but think of results of data-flow analysis as an example. See Section 8.3 for more information.
In Figure 15 we depict the generated ASF (see Section 3 for details on ASF). Let us take a look at the equation that was generated. First we see the T. In the TA-basis of Figure 14 we can see that this is a variable of type TRANSFORM. We recall that the variable can be instantiated with a function. T_W is the top traversal function and T_U and T_V are traversal functions for the body. Note that these expressions consist of two different tokens, displayed without any white space. White space is defined to be of sort LAYOUT, which is always optional in SDF. Moreover, U1 is a variable of sort U representing the subtree with root U and V2 is a variable of type V for the subtree V. The expression Attr1* is a variable representing a list of attributes which may contain values needed for specific transformations such as the introduction of new variables.
What is important to realize, is that we can substitute for the T any tool that an operator might define, for example, suppose we need a tool called foo. If we declare foo to be of type TRANSFORM it will match the variable T of type TRANSFORM. So we have now for foo the syntax foo_U, foo_V and foo_W available. The function foo_W operates on expressions of sort W. Therefore, the argument of the T_W is K U1 L V2 M--this is of type W. During traversal, the T_W eats itself through the grammar. The literals K, L, and M are not touched. For each sort we also generated variables that we can use. U1 is a variable of sort U and V2 is of type V. We see that the T distributes over its argument. We will return to the traversal idea itself in more detail in Section 5. For now it is important to realize that this process is so structured that it can be automated.
The TA-basis module that we displayed in Figure 14 is
imported again. In that module the sort name ANALYSE is declared.
Also the sorts DATA and BIN-OP are declared. We can see in
the context-free syntax of TA-basis that we can combine the data
using a binary operator. The {left} means that the grammar rule
is left associative. We can instantiate the generic sorts DATA
and BIN-OP at wish: if we need a test, then we can define the
DATA to be a Boolean and the BIN-OP a binary Boolean function.
The syntax in Figure 16 enables us to write expressions like
t_U(d,o,u)^{ }. This expression denotes the application of
test t on code fragment u, with result d if u
is a leaf, and sub-result combinator o. This is explained in more
detail in Figure 17.
We give generic analyzers two extra arguments so that an operator in the factory can instantiate them with the desired values. Like with the transformation syntax, we have for each sort a function symbol generated that has the sort name as a suffix in the form of an underscore.
The equation that has been generated from the grammar is the same as for the transformation as it comes to the distribution part. Indeed we see that the literals K, L and M disappeared. The o in between is a variable of type BIN-OP. The resulting output of the generic analyzer is a generic calculation: we have generic DATA and a generic operation BIN-OP in between. As soon as we instantiate these two we will get an actual calculation. Here A_W is the top analysis function and the others are for the body; o is an operator variable, like +, or and; d is a variable representing some default value, like 0 or true; the other symbols are as with the transform function. The difference with the transform function is that the analyze function does not preserve the context-free rule. Instead, all langauge constructions are mapped to one fixed type. Subresults are combined with a binary operator, represented by variable o. We note that in case of a grammar rule with only terminals at the left-hand side, the right-hand side of the equation we generate is a default value (d).
Consider Figure 18 containing the production rules for an artificial language called Cat. It is a dialect of ZOO. As can be seen from the lexical syntax, Cat contains the LAYOUT symbols: space, newline, and tab. Identifiers (ID) are upper-case characters mixed with numbers. We have expressions (EXP) of the form cat1, ..., cat8. We have three statements: a loop construct, an assignment construct and a conditional construct. We can combine statements to series of statements. A series of statements is a program. The Cat language is a dialect of ZOO. Later on we will see other dialects of ZOO that are also named after animals. Note that the grammar definition is not complete: there is, for instance, no sorts paragraph. We can generate this using the buttons that we see in the display. Note that we now have two more buttons than in Figure 12: one that generates a so-called native pattern language [92] (NatPatLang), and a button that performs all the tasks of this assembly-line called ApplyAll. If we hit the ApplyAll button, we obtain five windows. One containing the generated native pattern language, one containing the syntax for generic analyzers, on for its semantics, one for the syntax of the generic transformations, and finally one containing the semantics of the transformations. We only show the generated output of the Aeqs button in Figure 19. This is the semantics of the generic code analysers.
We see that eight ASF equations are generated. We generate for each
grammar rule one ASF equation, except for the LAYOUT production
rules since this sort is not in the abstract syntax tree to be analyzed.
Consider, for instance equation [default-6]. Its left-hand side
consists of the function name A_STAT and three arguments, the data
variable (called d here), the operator variable (called o),
and the assignment statement ID1 := EXP2. The variable ID1
represents any identifier in the Cat language and the variable
EXP2 represents any Cat expression. We generate these
variables in the native pattern language. Discussion of native patterns
is out of scope for this paper but for a detailed treatment we refer to
[92]. For now it suffices to think of native patterns as code
fragments with variables in them for matching. The nonterminals in the
assignment statement are translated to function calls in the right-hand
side of the equation. This right-hand side consists of a function
applied to the left-hand side of the assignment, a function applied to
the right-hand side of the assignment, and the binary operator variable
o in between them. As we can see, this is the generic set-up of
any analysis tool that combines the results on individual parts
of a program into one generic calculation. In the next section we show
how to obtain actual components from this generic one.
Our first target is to construct a component for the Cat language that counts the number of assignment statements in the code. This means that we present an alternative to the above discussed equation [default-6] so that the default equation will not be used. Note that [default-6] is responsible for the generic analysis of assignments. In Figure 20 we depicted the assignment counter component. We baptized it AssCnt.
We explain this tool. In the upper part of the module window we defined the syntax of this tool. We imported a language independent module called Tool-basis so that the generated generic transformations and analyzers are known to the tool. This Tool-basis imports the TA-basis, which imports the native pattern language. Everything that is relevant to the tool is known by this single import of the Tool-basis. We state that AssCnt is an analyzer, by declaring it being of the sort ANALYSE. We also define a function asscnt, that only takes a ZOO-term as single argument. This way we can specify the operator (+) and the default value (0), that are needed to give AssCnt the required behavior, in a separate equation (equation [0]) and call asscnt, instead of AssCnt, without reiteration of the operator and default value each time we call the assignment counter. Function AssCnt_ZOO is generated, using button Asyn. For the default value and the operator we initialize now default value zero and operator plus. Once we have done this we can further use the variables d and o since they will match the 0 and + because of equation [0]. Then in equation [1] we provide an alternative to equation [default-6]: we state that once we encounter some arbitrary assignment statement, it should be replaced by the number 1. Of course, this is an artificial example, but it shows exactly what has to be done in order to construct an actual component.
Next, we discuss the exaecution of the assignment counter on a simple Cat program. The program is displayed in Figure 21. Note that this figure contains a structured editor which is generated on the fly from the Cat grammar [67]. The editor contains three buttons, corresponding to the three example components we are going to implement. A first button is an analyzer to show the reader how to implement it, a second analyzer to show that the same generic analysers is used by as many analyzers as needed. The third is a transformation in order to illustrate how they are instantiated. For now, we explain the first button, which is the assignment counter.
We discuss the behaviour using parse trees representing the simple program
so that the reader can easily understand what happens during execution of
the component. First the concrete syntax is parsed according to the
Cat grammar. This yields the parse tree depicted in Figure 22.
We use a box around a sort name to indicate that the traversal of the tree
is at that point. So in the beginning we are at the top of the tree.
In Figure 23 equation [default-5] removes the literals
while, do, od, it distributes to the body of the while
and it puts an operator + in between. In Figure 24 we discuss
two steps: equation [default-3] distributes from the SERIES
level to the STAT level. Equation [default-1] replaces the
expression cat1 by the default value 0. At the appropriate
locations the plus signs are put in place. Then in Figure 25
the if statement is traversed using equation [default-7].
The literals if, then, else, fi are removed.
The sort name STAT is replaced by the sum operator and we
distribute over the body of the if. Note that this includes the
Boolean condition as well. In Figure 26 equation [default-1]
replaces the expression cat2 by the default value 0. Finally,
we have a situation that not only the default equations matches, but also
equation [1] that we defined in the assignment statement counter (see
Figure 20). It is used twice to replace two matching patterns
with the number 1. After normalizing this reducible expression,
we obtain 2 as a result. This is exactly the output of the assignment
statement counter tool that we implemented. The semantics of + is
specified in ASF and hence computation of the sums (0+(0+(1+1)))
are carried out as part of the reduction process (see Figure 27).
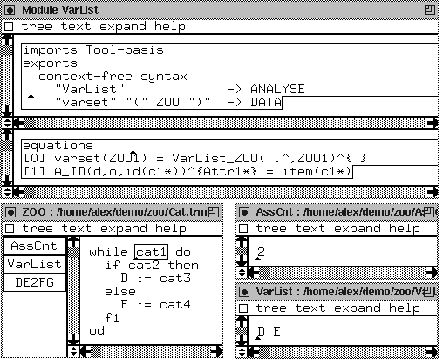 |
We can use the same generic analyzer for as many analysis
components as we need. The reason for this is that the generic functions
use the catamorphisms: A is a variable of type ANALYSE
so any instantiation will fit. In order to show this we have built
another component for Cat: it is a tool that provides a list of
the used variables in Cat programs. In Figure 27 we give
an overview: the VarList tool, the example program and the output
of the AssCnt and VarList buttons in separate windows.
We see that the structure of the variable listing component is exactly
the same as the first one. The instantiation is specified in equation
[0]: for the default value we have the empty word, represented
by a white space in Figure 27. The operator is concatenation.
We have chosen the circumflex notation, but this could have been anything
else. Then in equation [1] we provide alternative behaviour for
equation [default-0] of Figure 19. In this equation we
see two functions: id and item. We explain them. In fact,
for every lexically defined sort (so also ID and ITEM)
the ASF+SDF Meta-Environment generates a corresponding function with the sort name in
lower case characters. Such a function has a predefined sort CHAR*
as domain and the range is the lexically defined sort. So in the above
cases two functions are generated under the surface:
"id" "(" CHAR* ")" -> ID
"item" "(" CHAR* ")" -> ITEM
In the parse tree the lexical syntax form the leaves. But also the leaves have structure, and sometimes it is desirable to manipulate the lexical structure just as we wish to manipulate the context-free structure. The lexical access functions serve the purpose of being able to do this. So, for instance, multiplying by ten can be implemented in the ASF+SDF Meta-Environment by using these generated functions by concatenating a zero to the end of a number. In the example, the lexical access functions are used to carry out a type conversion (from ID to ITEM).
Now we discuss a transformation to explain the instantiation of the generic transformations. We depict the result of pressing the Teqs button (Figure 18) for the Cat dialect in Figure 28. We see that eight equations are generated. They implement the complete traversal functionality for Cat programs.
We implemented a tool that transforms an arbitrary assignment statement beginning with D := to F := and that transforms each identifier E into the identifier G. So we see that we transform on two levels: the assignment statement level and the identifier level. Of course this is an artificial tool. We present it here to explain the way the transformation components work. See Figure 29 for the complete tool specification. We use the same example program of Figure 21 to explain this so-called DE2FG tool. We display the example program plus its output of the DE2FG component in Figure 30.
The syntax of transformation components is like the analyzers
that we already discussed, only simpler: it is not necessary to
initialize a transformation with default values. For convenience's
sake we implemented the syntax of transformations identical to that of
analysers. So we have an extra function de2fg without underscores
for usage in the outside world. The semantics of DE2FG is as
follows. In equation [1] we have an alternative equation to
equation [default-0] on the identifier level. We stated that
when we find an identifier named E we rename it to G.
In equation [2] (on the statement level), we deviate from the
default traversals for assignment statements that start with an identifier
D. This equation transforms each D occurring in the left-hand
side of an assignment to an F.
Next we explain, using the tree representation that we saw before, the execution of the DE2FG component for the simple example program. Figure 22 is the first step for our transformation. We are at the top of the tree and now we start traversing the tree with the DE2FG tool. In Figure 31 we see that not much happens in the tree: there is only distribution over the while performed by equation [default-5] (observe that the terminals are not removed during transformations). We move to Figure 32: on the expression cat1 nothing happens so that part is finished using equation [default-1]. With equation [default-3] we distribute from the SERIES to STAT level. Then in Figure 33 we distribute through the body of the if statement using equation [default-7]. In Figure 34 we arrive at a point where not only default equations match, but also a hand written one: equation [2] depicted in Figure 29. Since the latter does not have default status, it will be applied. We see that the D := cat3 is changed into F := cat3. Since our handcrafted equation does not fit the other assignment it will be treated with equation [default-6]. Using equation [default-1] the expression cat2 is traversed without a change. Then our handwritten equation [1] is applied in Figure 35 in order to rename E to a G. With default equation [default-1] we traverse through the EXP (representing cat4) and we are done.
We have explained what happens when our architecture is used to implement transformations and analysis functions, we will see in the next section how we can reuse components.
An, in our opinion, very important consequence of the LP-PP
approach that we discussed in Section 4 is that
the generated components should be maximally reusable and thus easily
maintainable. We sketched the situation in Figure 36.
In Section 4 we have seen that components consist of a
shared part that is generated from a grammar G containing the generic
rules. In Section 5 we saw that the handcrafted parts
![]() containing problem specific rules are usually small.
Suppose that we want to reuse the components
containing problem specific rules are usually small.
Suppose that we want to reuse the components ![]() in
a different dialect G'. Then we usually only have to regenerate the
generated part and we do not have to modify any of the handcrafted parts.
The purpose of this section is to illustrate this.
in
a different dialect G'. Then we usually only have to regenerate the
generated part and we do not have to modify any of the handcrafted parts.
The purpose of this section is to illustrate this.
Before we continue, let us first give a real-world example to make
this apparent. Suppose we have a renovation factory to migrate certain
company specific COBOL 74 code to a dialect of COBOL 85. Suppose that
for another company we have the same problem to solve. The new customer
has another COBOL 74 dialect. Suppose, for the argument, that in the
PROCEDURE DIVISION a DECLARATIVES section has been added.
We extend the grammar G with this knowledge thus obtaining G'.
Then we regenerate the generic part of the components. Since we
are sure that the components ![]() do not affect the
DECLARATIVES keyword (for, it was not even in the grammar G) they
do not need to be adapted. They use the newly generated functions and
the original handcrafted parts and work now on the new grammar. It is
not necessary to make a single change to the components. Of course, the
second grammar G' is an extension of the first grammar, so the reader
might get the impression that our approach only works for extensions.
In fact, we use this simple example to give the reader a first impression.
In a more elaborate example we will show that reuse is not limited to
the extension case. In fact, we discuss a dialect that is neither an
extension nor a subset: both dialects share just one production rule.
do not affect the
DECLARATIVES keyword (for, it was not even in the grammar G) they
do not need to be adapted. They use the newly generated functions and
the original handcrafted parts and work now on the new grammar. It is
not necessary to make a single change to the components. Of course, the
second grammar G' is an extension of the first grammar, so the reader
might get the impression that our approach only works for extensions.
In fact, we use this simple example to give the reader a first impression.
In a more elaborate example we will show that reuse is not limited to
the extension case. In fact, we discuss a dialect that is neither an
extension nor a subset: both dialects share just one production rule.
We define a dialect of ZOO, called Dog for which we reuse the components that we implemented for the Cat dialect of ZOO. It turns out that we can completely reuse any component as long as the grammar of the new language does not affect the part of the original grammar on which the component is working. Let us stress that although this example is artificial, we applied the discussed approach successfully to the myriad of dialects of COBOL. We depict the grammar of Dog in Figure 37.
Our definition of a dialect is that both grammars should have at least one production rule in common. Note that only the production rule
ID ":=" EXP -> STAT
is the same both in Cat and Dog. See Figure 18 for the grammar of Cat. Although the sorts ID, EXP, STAT occur in both languages, they are not the same. In fact, we have other LAYOUT (no tabs allowed), different identifiers (no numbers allowed), disjoint expressions ( dog1, ..., dog8 instead of cat1, ..., cat8), different statements (no if, no while but print and foreach), and no series of statements separated by a semi-colon, but sentences ending in a period. Since the grammars for Cat and Dog share one production rule we still call Dog and Cat dialects of ZOO.
We press the button ApplyAll (see Figure 37) for the Dog grammar, in order to generate the syntax and semantics of the new generic components plus the new native pattern language. We load the obtained modules in the ASF+SDF Meta-Environment. Since we have attached buttons for the components AssCnt, VarList and DE2FG to the editor, the components that we just constructed are being loaded when we open an editor for a Dog program. We can reuse all components originally implemented for Cat programs, for the Dog dialect without a single change. This is possible since the grammar of Dog does not affect the handwritten part of Cat on which the three components are working. Of course, other parts differ. This is not a problem since for the changed parts we generated the new behaviour for the generic components. We displayed the generated output of the Aeqs button for Dog in Figure 38. We show with the example program in Figure 39 what happens, so that the reader can check our claims.
Let us discuss the traversal of the little Dog program in the same way as we did for the simple Cat program (only shorter). We will show that the AssCnt button will print the number 2 since there are two assignments in the Dog program. We depicted the parse tree in Figure 40. The program is just a foreach sentence. So, only equation [default-7] of Figure 38 applies, and its effect is that the keywords foreach, to, and do are removed, while the generic analysis functions now apply to the level below. We have now four positions where equations fit: ID, EXP, another EXP and the second level SENT. Those cases are dealt with by the following equations: equation [default-1] for the ID representing D; two times equation [default-0] for dog1 and dog2; and equation [default-4] for the sentence that is in the foreach. The first three applications result in a default value zero combined using plus operators. The remaining application distributes over the sentence. So now equation [default-4] applies and we reached the left-first STAT in Figure 40. Furthermore, we are at the third SENT. By two more applications of equation [default-4] we end up in the situation that we only have to deal with the three STAT parts in the figure. On the first two the nondefault equation [1] of the assignment counter that we depicted in Figure 20 applies. So at those two positions the number 1 is substituted for the assignment. On the last STAT the default equation that we generated for Dog applies: equation [default-6]. So the print keyword is removed and for the EXP representing dog5 a zero is substituted. The resulting term is a calculation that evaluates to 2. We can do the same for the VarList and the DE2FG components. We leave this as an exercise for the reader.
Although this example is quite artificial, it clearly shows that when dealing with substantially different dialects of a language, we can still reuse components that have handcrafted parts on shared constructions in a black box fashion: no change of the component is necessary. In the every-day-practice of reengineering COBOL with its extensions, like CICS and/or SQL we use this technology fruitfully. Once we constructed a tool for a customer using a certain dialect, we can reuse the components effortlessly for other dialects in other projects. As a consequence, we have experienced that our renovation components are insensitive to dialects. Software renovation factories that are not addressing dialects issue somehow, are likely to run into huge grammar maintenance problems. See [17] for more information.
The LAYOUT is similar to the LAYOUT in Cat. The identifiers may contain a colon and an equality sign. We have only ony identifier. It looks like an assignment: Example:=Tricky. We have BLOCK structures in Rat, consisting of STATs that are separated by the := separator. Furthermore, we have the same rule for the assignment as with Cat and Dog. So also here the intersection of the two grammars as minimal as with Cat and Dog. We do have a while statement and a conditional statement, but with BLOCKs instead of SERIES. Of course, this language is beyond zoo--it is just there to make the point of robustness.
We push the ApplyAll button (see Figure 41) and we load the new dialect of ZOO in the ASF+SDF Meta-Environment. We note that the ASF+SDF Meta-Environment has no problems with the Rat grammar: on the fly a parser is generated and a structured editor, etc. We display the outcome of the Aeqs button in Figure 42 so that the reader can inspect the generated generic analysis equations.
We open an editor containing a Rat program (Figure 43). Since we made buttons for the three components, they are automatically loaded. The purpose of this dialect is to show that although it becomes quite difficult to count the assignment statements, the components that we originally developed for Cat can be reused without a single change. Note that the DE2FG component is the identity on the example Rat program.
We have made a Rat program that is not easy to parse (for humans), and for which a simple lexical tool will most certainly break down. For instance, the Unix command
grep := Rat.trm | wc -l
returns 10. Similar commands return correct values for the other example programs (see Figures 21 and 39). We display the program plus the results of the components AssCnt and VarList in Figure 43. We see that the result of the AssCnt button yields 4. Let us analyse the Rat program and conclude that our AssCnt component is returning the correct answer.
The reason that it is difficult for humans and lexical tools to count the number of assignment statements is that we used the := token in many different contexts. Therefore, we depicted in Figure 44 the parse tree of the Rat program. We abbreviated Example:=Tricky to e:=t. We discuss the traversal of the AssCnt component. Note that it uses the generated analysis equations from the Rat grammar (see Figure 42) plus the equations depicted in Figure 20. Since the program is a simple if we start with equation [default-7]. It will remove the terminals (if, then, else, and fi). Then it adds the results of the body of the if: the EXP, and two BLOCKs. The EXP is replaced by zero due to equation [default-1]. The two BLOCKs are traversed with [default-4] and [default-3] respectively. Then we enter the left-first STAT and equation [1] of the AssCnt component applies: a 1 is the replacement. The BLOCK is traversed using a default equation and we enter the second STAT, which is also replaced by 1 by equation [1] of the AssCnt component. In the right-hand side of Figure 44 we enter a while statement. Using equation [default-6] we throw away the terminals and enter the body of the while. As with the if, the EXP is replaced by 0 and the two STATs are replaced by a 1 because of the nondefault equation [1] of the assignment counter. The resulting term evaluates to 4.
The other components also work for the Rat language. So, we see that although it becomes quite complex to analyze the program using lexical techniques, the approach that we propose in this paper is not only easy and reusable, but also robust.
As an illustration we discuss in this paper a number of real-life components that are useful in restructuring COBOL code and we discuss components to migrate COBOL 74 code to COBOL 85 code. So, we distinguish components to analyze, components to restructure, and components to migrate. We use analysis components to decide whether or not certain migration or restructuring components should be activated, e.g., if the COBOL 74 special register CURRENT-DATE does not appear in original code, it is not necessary to perform a CURRENT-DATE transformation. What all these components have in common is that they are generated and that their specification is straightforward using the methods discussed in Section 5.2. The effort to construct them is usually measured in minutes. Moreover, they are maximally reusable, and robust.
In Section 8.1 we briefly discuss the danger of underestimating simple transformation tasks. Once we have an idea of these dangers, we discuss in Section 8.2 the construction of two components using the implementation strategy that we propose in this paper. In Section 8.3 we describe a more sophisticated restructuring which inserts the missing explicit scope terminators for conditional constructs in COBOL code. In Section 8.4 a migration component which deals with the CURRENT-DATE transformation is discussed.
Suppose we have the simple task of removing the words UPON CONSOLE from the COBOL DISPLAY statement in a complete COBOL system. This can be implemented in a one-liner using our approach. Of course, we need the grammar, a pretty printer, the generic transformations, we need to pre and postprocess the COBOL code. So one could argue that this can be done more easily and cheaper using a simple lexical tool, or even using a text editor macro. For, we only have to remove the words UPON CONSOLE in code like:
DISPLAY '** BEGIN PROGRAM' UPON CONSOLE.
In fact, we carried out this task (among others) for a customer on a COBOL/SQL system using our approach. We will show in this section some anonymized code fragments of this system. On their COBOL/SQL system we applied the following command that removes the UPON CONSOLE from the system:
perl -p -e "s/UPON CONSOLE//g" * | less
to show the danger of such careless operations. This perl command [104] shows the result of removing the words UPON CONSOLE in all the files of the system. This is a typical simple tool: it is a lexical tool, it is a one-liner, and there is no need to do anything fancy with the code to get things going. Application of this command to the system has a devastating effect. The result of the above command leads to a system that is not at all executable anymore. The reason is that each line of this system has trailing comments, like in this line:
00188 DBO02-002-XXX UPON CONSOLE XXXXXXXX
So the line is transformed into:
00188 DBO02-002-XXX XXXXXXXX
The name of the file (XXXXXXXX) which first was comment is turned
into code by the simple tool. The system will not compile anymore.
In order to solve this we can invoke another perl command that
replaces UPON CONSOLE by spaces. But suppose that there are two
spaces between UPON and CONSOLE, then we need an additional
command. As we can see, this simple tool breaks down immediately.
Whatever the next try will be, in the end it will boil down to a form
of preprocessing the system code. So let us suppose that we have
preprocessed the code so that trailing comments are not a problem.
For preprocessing COBOL code we refer to [15] where we discuss
how to obtain a COBOL grammar for reengineering purposes.
Let us look at the next problem. In some of the files the UPON CONSOLE is already removed. This is indicated in the files as follows:
00017 * - UPON CONSOLE REMOVED
which is transformed by a simple tool into:
00017 * - REMOVED
It is not a good idea to remove comments while restructuring. So, the simple tool needs modification to prevent changing comments. We have at least two flavours for comments (using a or a / in the seventh column) so the tool gets more complicated. Now suppose we have solved that also. Let us look at the next problem.
00308 IF OKAY
00309 PERFORM READ-CARD
00310 IF AVAILABLE
00311 PERFORM INITIALIZE-INPUT
00312 ELSE
00313 DISPLAY 'OI120 NOT AVAILABLE'
00314 UPON CONSOLE.
The latter UPON CONSOLE will be removed and the result is a separator period that ends the nested IF on a single line:
00308 IF OKAY
00309 PERFORM READ-CARD
00310 IF AVAILABLE
00311 PERFORM INITIALIZE-INPUT
00312 ELSE
00313 DISPLAY 'OI120 NOT AVAILABLE'
00314 .
This is not in compliance with the coding style of the company. Moreover, loose separator periods are a source of errors. So the simple tool needs to be modified to take care of this issue: it should put the separator period right after the display statement. As we can see, the simple tool is no longer simple. A variant of the above problem is present in the code below:
00230 IF XXX-XXXXX = '1'
00231 DISPLAY '***********************************************'
00232 UPON CONSOLE
00233 DISPLAY '** PROGRAM XXX **'
00234 UPON CONSOLE
00235 DISPLAY '** BATCH XXX IS OKAY **'
00236 UPON CONSOLE
00237 DISPLAY '***********************************************'
00238 UPON CONSOLE
00239 CALL 'XXXXX'.
The simple tool will replace this with:
00230 IF XXX-XXXXX = '1'
00231 DISPLAY '***********************************************'
00232
00233 DISPLAY '** PROGRAM XXX **'
00234
00235 DISPLAY '** BATCH XXX IS OKAY **'
00236
00237 DISPLAY '***********************************************'
00238
00239 CALL 'XXXXX'.
Also this is not in compliance with coding styles of the company. The empty lines should be removed. So the simple tool needs to take care of this as well. Another problem occurs when the following code is changed:
00820 DISPLAY XRST-MSG-XXXX UPON CONSOLE.
00821 DISPLAY XRST-MSG UPON CONSOLE.
00822 DISPLAY XRST-MSG-XXXX UPON CONSOLE.
This results in:
00820 DISPLAY XRST-MSG-XXXX .
00821 DISPLAY XRST-MSG .
00822 DISPLAY XRST-MSG-XXXX .
Again, this is not in compliance with coding style of the company. So this should be solved as well. As we can see, simple tools turn rapidly into very complicated tools, containing preprocessing, pretty printing, grammar knowledge and such in an ad hoc way. As soon as the next `simple' task needs to be performed a lot of (other) problems need to be solved in the next tool to implement the so-called simple functionality.
It is a better idea to have a structured approach towards transformations, even the ones that look deceptively simple at first sight. We argue that there is no such thing as a simple tool that is able to perform a system-wide transformation in a controlled way. We note that simple maintenance changes are underestimated in general: in [38] we can read that research at a software maintenance organization pointed out that 55 percent of one-line changes were in error before code reviews were introduced. The belief that a change will be easy to do correctly makes it less likely that the change will be done correctly [108, p. 236].
In Figure 45 we display the mct component; mct stands for MOVE CORR transformation. B-exp stands for basic expression which can be a variable, a string, a literal, etc. Data-name stands for a variable name. From here onwards -p after a variable means one or more occurrences of it.
Only at the statement level (Stat) we want special behavior: a MOVE CORR with one or more Data-names should be changed into a MOVE CORR with statement connectors THEN. This is recursively defined in equation [1]. In Figure 46 we give a simple example program called MCT-DEMO. the buttons at the left-hand part of the window correspond to components we used.
The code is very simple, and the PROCEDURE DIVISION contains one paragraph, with one sentence. When we press the mct button, we obtain the desired output. We depict this in Figure 47. As we can see, the compound sentence is divided into parts with THEN statement connectors.
Next we discuss a component that migrates the THEN statement connector (COBOL 74 specific) into multiple statements. In COBOL/370 (a COBOL 85 dialect) THEN as a statement connector is obsolete. We have to change three equations by hand.
The abbreviation rth stands for remove THEN. Equations [1-3] treat all the different cases of occurrences of THEN as a statement connector: at the beginning of a sentence [1] and at the end of a sentence [2]. Equation [3] takes care of the THEN inside IF-constructions. Note that rth does not remove the THEN which is part of an IF statement. We mention for the sake of completeness that the context-free grammar rule for THEN on the Stat level in SDF is:
Stat "THEN" Stat -> Stat {right}
Where {right} indicates that the binary statement connector
THEN is right associative. Therefore, it is not necessary to process
the Stat1 subtree in the right-hand sides. Recursively, the
statements which form a sentence or a list of statements are processed
and if a THEN connector is found it is removed.
We press the rth button in Figure 47 and we obtain the
in Figure 49. We also explain why it is useful to transform
and migrate in this way.
Pressing the rth button removes the THEN statement connector. Now we explain why we do these things in small steps. First, mct transforms the COBOL 74 code into COBOL 74 code with a statement connector. Then rth removes the statement connectors. We use an extra phase because we want to keep components as small as possible. It is possible to equip mct with the extra functionality so it could make from one statement an arbitrary number of statements, which is in this example from one to three, however this would make the component more complicated. In practice, transformations from n to m statements often occur. Therefore, we perform such transformations in two phases: first we use THEN as a statement connector to keep the number of statements constant and in the end we use the rth transformation to remove the connectors. Another example of the use of rth can be found in Section 8.4; in that example we use rth to transform one statement into two. In fact, what we see here is a tiny renovation assembly line in a renovation factory. Since the purpose of this paper is not to explain renovation problems but to explain how we implement components for renovation factories to solve such problems we will not dive into the very important subject of assembly lines. For more details on assembly lines we refer to some of the papers mentioned in Section 1.1. Apart from that, it is not a new insight that it is better to have many small understandable steps rather than a large single transformation. In [11] this approach is also advocated and applied.
There are not only END-IF terminators but also, e.g., END-READ, END-STRING, and END-WRITE scope terminators in COBOL 85 dialects. We will discuss the construction of a restructuring component that transforms the implicit scope terminators for conditionals into an END-IF. We note that other implicit to explicit scope termination components are constructed analogously, but simpler since their grammar is simpler. Typically, those components are one-liners using our approach.
First, we discuss a fragment of the COBOL grammar in SDF. These grammar rules recognize COBOL 74 programs without scope terminators as well as COBOL 85 programs with or without scope terminators (this is an example of an I/O grammar depicted in Figure 11). The grammar of the conditionals is rather complicated, due to the design decision that COBOL should resemble natural language. We recall the scope delimiting rules from the ANSI Standard [2]: The scope of the IF statement may be terminated by any of the following:
We have expressed the above rules in our context-free grammar of COBOL. Let us first explain that conditional expressions in COBOL 85 dialects come in three flavors: the good, the bad, and the ugly. The good ones use the explicit scope terminator END-IF (rule a). The bad ones come in nested conditional COBOL constructs and seem, due to the nature of the implicit scope termination rules, to be incomplete (rule b). The expression IF L-exp Stat1 ELSE Stat2 is an example of a bad conditional. The ugly ones are terminated with a separator period (rule c).
We explain the grammar fragment we displayed in Figure 50. Since also normal statements can occur in the body of an IF statement, we first created a nonterminal called Cond-body in which those statements occur, possibly ended by a bad conditional (called Bad-cond). Then we are able to define what a Bad-cond is: an IF statement that is not explicitly terminated and that can contain such not terminated IF statements as well. Then we say that with the addition of an END-IF we can turn an incomplete IF statement into a complete Statement, called Stat. Finally, we express in the last two rules how to complete an IF with the addition of a separator period. Let us recall that a COBOL sentence (Sent) is one or more statements followed by a separator period. Note that this implies that in COBOL 74 dialects an IF can only be the end of a sentence so that an IF statement does not exist (see [89] for details on such issues).
Note that the production rules for the IF statement are only a selection of a complete modular grammar definition of COBOL in SDF (see [15] for more details on COBOL grammars). An example of a code fragment that can be parsed by the above grammar fragment and that contains all three conditional flavors is the not transformed version of the slight-slot program in Figure 52; we indicated the three possible IF statements in there, with good, bad, and ugly tags.
We discuss the transformation component that turns bad and ugly conditionals into good ones; it is a tool called aei which stands for add END-IF. It is the component that inserts an END-IF at the appropriate places. We displayed the hand-written part of this component in Figure 51.
We have to find an alternative for three of the generated generic equations. This is not surprising, since we have three places in the grammar where an END-IF is missing and an implicit scope terminator takes care of the scope of the IF statement. They are the one that defines Bad-cond (that one misses an explicit scope terminator) and the two that take care of the separator period (they use a dot as terminator instead of an END-IF). Furthermore, we need an auxiliary component that removes a separator period from a sentence; it is called rsp which stands for remove separator period .
In Figure 52 we have depicted a COBOL program that shows the word SLINGSHOT. Depending on the value of X the program's output is either SLIGHT or SLOT. We tagged the various IF statements with good, bad, and ugly (of course now the program does not parse anymore in the window). At the right-hand side of Figure 52 we display the result of pressing the aei button. Let us briefly discuss how aei processes the slight-slot program so that the implementation of aei becomes clear.
 |
In order to explain what happens exactly, we should display the syntax tree of this code fragment, and walk the tree as we did with the Cat example in Section 5.2. Since the trees become quite large, this is not possible. Therefore, we describe what happens without a parse tree.
First, the generated function aei_Program is applied to the
example program. Via the generated traversal functions we will reach
the relevant parts of the code for aei where it will perform
the desired modifications. Suppose we arrived at the ugly IF
in this way. Then we recognize that this piece of code is a COBOL sentence. It matches with equation [3] of Figure 51.
This results in removing the separator period by rsp and then
adding END-IF followed by a separator period as can be seen in the
right-hand side program. We continue with the remaining construction
inside the ugly IF. This happens to be a Cond-body consisting
of a Stat and a Bad-cond. On a simple Stat the function
aei is having default behaviour. We arrive at the bad conditional
Bad-cond. According to equation [1] it adds an END-IF
and continues with the inside of the second IF. In the body of
that IF we find a simple statement and a good conditional, which
is also a statement. Now the body of that conditional is examined.
Since the body consists of only two simple statements we are done.
The component cda (CURRENT-DATE analyzer) checks whether or not CURRENT-DATE occurs in a program. We display the handwritten equations for cda in Figure 53.
Equation [0] takes care of the correct initialization of the default value d and the binary operator o (see Section 5.2 for details). We introduce this extra equation to give the cda component its default values. Note that the default is false so we assume no occurrences of CURRENT-DATE by default. The operator or is used to combine the results of the cda analyzer on subtrees. Equation [1] recognizes a MOVE CURRENT-DATE TO expression and returns true.
We will use cda in the definition of the cdt component (this stands for CURRENT-DATE transformer). Before we display its equations, we discuss a way to implement the CURRENT-DATE transformation, we do this using example programs depicted in Figure 54.
The input program is the program on the left of Figure 54. This programs displays the current date as day, month, and year separately. In the IBM migration guide [49], it is proposed to change the type of variable TMP from PIC X(8) to X(6) and to change MOVE CURRENT-DATE into an ACCEPT statement. This is expressed in the right-hand side of Figure 54. This solution breaks down as soon as TMP is used in a context assuming the original format X(8). H-DATE is such a context. The output the transformed program yielded on the date 04/14/97:
DAY = 41
MONTH = 97
YEAR =
Obviously this is entirely wrong: there is no DAY 41, no MONTH equals 97, moreover the YEAR field is empty. We observed that in more recent versions of the IBM Migration guide, this erroneous transformation advise has been corrected.
Our cdt component returns the program that we displayed in Figure 55. It introduces a fresh variable F-Date to store DATE in its (fresh) subfields: F-YY, F-MM, F-DD. Subsequently, we simulate the format of CURRENT-DATE by using the STRING statement. In this way the format of TMP is exactly the same as before the migration so the abovementioned error will not arise.
Next, we discuss the construction of cdt. We depicted its
four equations in Figure 56. Equation [0] defines
the function cdt_Program under the condition that no
CURRENT-DATE occurs in Program: then cdt_Program
just returns the input unchanged. Equation [1] defines
cdt_Program on Program0 to be the rth_Program (remove
THEN, see Figure 48) of another program Program1
under the following conditions. First, there is a CURRENT-DATE,
this is checked by cda_Program. Second, the input program is
extended with a fresh record, yielding Program1. The function
id is another example of a lexical access function that we already
saw in Section 5.2. We use it here to inject identifiers
into attributes. We use Attr* as memory so that we can both
declare the fresh variables in the working storage section and
use the fresh variables in the PROCEDURE DIVISION. So,
we make a change at two different locations in the program. This means
that we perform a global transformations using the Attr* mechanism.
We could also have implemented this transformation using a global pattern.
For examples of global patterns we refer to the papers we mentioned in
Section 1.1. Equation [2] takes care of the
insertion of the fresh variables in the WORKING-STORAGE SECTION.
It matches the one or more present records in that section with
variable Data-desc-p and it adds the fresh record F-Date
to it. Finally in equation [3], on the statement level,
cdt matches the MOVE CURRENT-DATE TO phrase and returns a new
statement consisting of the ACCEPT part and the simulation part.
Note that the THEN is removed in equation [1]. This is
done to keep the number of statements a constant while transforming
(see Section 8.2 for details).
Of course, cdt is not flawless: in order to migrate automatically, we have to know that the variables are fresh, so we have to check that with an analyzer. If there are nonfresh variables, we should make them fresh automatically. We will not describe these extra components here since the purpose of the example transformation is to illustrate how to implement components for a software renovation factory and not how to implement the ideal assembly line that automatically solves the CURRENT-DATE problem in all its facets. We are aware of the flaws of cdt and we can construct an assembly line that is more sophisticated. This assembly line uses the methods described in this paper.
Let us conclude this section with the remark that a component that takes care of the transformation of the OS/VS COBOL TIME-OF-DAY special register to the COBOL/370 TIME special register can be constructed analogously to the CURRENT-DATE transformation.
We hope to have shown that our approach allows the rapid construction of reliable components with advanced functionality. Also, we belief that a software renovation factory is an appropriate paradigm to deal with massive amounts of code, and that the generation of components for such a factory is of economic importance.