#include <ScalarEvolutionExpressions.h>

Inheritance diagram for llvm::SCEVAddRecExpr:

Collaboration diagram for llvm::SCEVAddRecExpr:

Public Member Functions
const SCEV *	getStart () const

const Loop *	getLoop () const

const SCEV *	getStepRecurrence (ScalarEvolution &SE) const

bool	isAffine () const

bool	isQuadratic () const

void	setNoWrapFlags (NoWrapFlags Flags)

const SCEV *	evaluateAtIteration (const SCEV *It, ScalarEvolution &SE) const

const SCEV *	getNumIterationsInRange (ConstantRange Range, ScalarEvolution &SE) const

const SCEVAddRecExpr *	getPostIncExpr (ScalarEvolution &SE) const

const SCEV *	delinearize (ScalarEvolution &SE, SmallVectorImpl< const SCEV * > &Subscripts, SmallVectorImpl< const SCEV * > &Sizes) const

Public Member Functions inherited from llvm::SCEVNAryExpr
size_t	getNumOperands () const

const SCEV *	getOperand (unsigned i) const

op_iterator	op_begin () const

op_iterator	op_end () const

Type *	getType () const

NoWrapFlags	getNoWrapFlags (NoWrapFlags Mask=NoWrapMask) const

Public Member Functions inherited from llvm::SCEV
	SCEV (const FoldingSetNodeIDRef ID, unsigned SCEVTy)

unsigned	getSCEVType () const

Type *	getType () const

bool	isZero () const

bool	isOne () const

bool	isAllOnesValue () const

bool	isNonConstantNegative () const

void	print (raw_ostream &OS) const

void	dump () const

Public Member Functions inherited from llvm::FoldingSetImpl::Node
	Node ()

void *	getNextInBucket () const

void	SetNextInBucket (void *N)

Static Public Member Functions
static bool	classof (const SCEV *S)
	Methods for support type inquiry through isa, cast, and dyn_cast: More...

Static Public Member Functions inherited from llvm::SCEVNAryExpr
static bool	classof (const SCEV *S)
	Methods for support type inquiry through isa, cast, and dyn_cast: More...

Friends
class	ScalarEvolution

Additional Inherited Members
Public Types inherited from llvm::SCEVNAryExpr
typedef const SCEV const	op_iterator

Public Types inherited from llvm::SCEV
enum	NoWrapFlags { FlagAnyWrap = 0, FlagNW = (1 << 0), FlagNUW = (1 << 1), FlagNSW = (1 << 2), NoWrapMask = (1 << 3) -1 }

Protected Member Functions inherited from llvm::SCEVNAryExpr
	SCEVNAryExpr (const FoldingSetNodeIDRef ID, enum SCEVTypes T, const SCEV const O, size_t N)

Protected Attributes inherited from llvm::SCEVNAryExpr
const SCEV const	Operands

size_t	NumOperands

Protected Attributes inherited from llvm::SCEV
unsigned short	SubclassData

Detailed Description

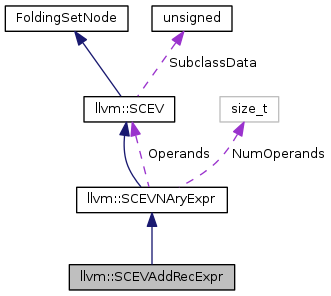
SCEVAddRecExpr - This node represents a polynomial recurrence on the trip count of the specified loop. This is the primary focus of the ScalarEvolution framework; all the other SCEV subclasses are mostly just supporting infrastructure to allow SCEVAddRecExpr expressions to be created and analyzed.

All operands of an AddRec are required to be loop invariant.

Definition at line 283 of file ScalarEvolutionExpressions.h.

Member Function Documentation

static bool llvm::SCEVAddRecExpr::classof ( const SCEV * S )

inlinestatic

Methods for support type inquiry through isa, cast, and dyn_cast:

Definition at line 351 of file ScalarEvolutionExpressions.h.

References llvm::SCEV::getSCEVType(), and llvm::scAddRecExpr.

const SCEV * SCEVAddRecExpr::delinearize	(	ScalarEvolution &	SE,
		SmallVectorImpl< const SCEV * > &	Subscripts,
		SmallVectorImpl< const SCEV * > &	Sizes
	)		const

Splits the SCEV into two vectors of SCEVs representing the subscripts and sizes of an array access. Returns the remainder of the delinearization that is the offset start of the array.

Splits the SCEV into two vectors of SCEVs representing the subscripts and sizes of an array access. Returns the remainder of the delinearization that is the offset start of the array. The SCEV->delinearize algorithm computes the multiples of SCEV coefficients: that is a pattern matching of sub expressions in the stride and base of a SCEV corresponding to the computation of a GCD (greatest common divisor) of base and stride. When SCEV->delinearize fails, it returns the SCEV unchanged.

For example: when analyzing the memory access A[i][j][k] in this loop nest

void foo(long n, long m, long o, double A[n][m][o]) {

for (long i = 0; i < n; i++) for (long j = 0; j < m; j++) for (long k = 0; k < o; k++) A[i][j][k] = 1.0; }

the delinearization input is the following AddRec SCEV:

AddRec: {{{A,+,(8 * m * o)}<for.i>,+,(8 * o)}<for.j>,+,8}<for.k>

From this SCEV, we are able to say that the base offset of the access is A because it appears as an offset that does not divide any of the strides in the loops:

CHECK: Base offset: A

and then SCEV->delinearize determines the size of some of the dimensions of the array as these are the multiples by which the strides are happening:

CHECK: ArrayDecl[UnknownSize][m][o] with elements of sizeof(double) bytes.

Note that the outermost dimension remains of UnknownSize because there are no strides that would help identifying the size of the last dimension: when the array has been statically allocated, one could compute the size of that dimension by dividing the overall size of the array by the size of the known dimensions: m * o * 8.

Finally delinearize provides the access functions for the array reference that does correspond to A[i][j][k] of the above C testcase:

CHECK: ArrayRef[{0,+,1}<for.i>][{0,+,1}<for.j>][{0,+,1}<for.k>]

The testcases are checking the output of a function pass: DelinearizationPass that walks through all loads and stores of a function asking for the SCEV of the memory access with respect to all enclosing loops, calling SCEV->delinearize on that and printing the results.

Definition at line 7121 of file ScalarEvolution.cpp.

References llvm::dbgs(), DEBUG, findGCD(), llvm::ScalarEvolution::getAddExpr(), llvm::ScalarEvolution::getAddRecExpr(), llvm::ScalarEvolution::getConstant(), getLoop(), llvm::ScalarEvolution::getMinusSCEV(), llvm::ScalarEvolution::getMulExpr(), llvm::SCEVNAryExpr::getNoWrapFlags(), getStart(), getStepRecurrence(), llvm::SCEVNAryExpr::getType(), isAffine(), llvm::SmallVectorTemplateBase< T, isPodLike< T >::value >::push_back(), and llvm::SmallVectorTemplateCommon< T >::size().

const SCEV * SCEVAddRecExpr::evaluateAtIteration	(	const SCEV *	It,
		ScalarEvolution &	SE
	)		const

evaluateAtIteration - Return the value of this chain of recurrences at the specified iteration number.

evaluateAtIteration - Return the value of this chain of recurrences at the specified iteration number. We can evaluate this recurrence by multiplying each element in the chain by the binomial coefficient corresponding to it. In other words, we can evaluate {A,+,B,+,C,+,D} as:

A*BC(It, 0) + B*BC(It, 1) + C*BC(It, 2) + D*BC(It, 3)

where BC(It, k) stands for binomial coefficient.

Definition at line 802 of file ScalarEvolution.cpp.

References BinomialCoefficient(), llvm::ScalarEvolution::getAddExpr(), llvm::ScalarEvolution::getMulExpr(), llvm::SCEVNAryExpr::getNumOperands(), llvm::SCEVNAryExpr::getOperand(), getStart(), and llvm::SCEVNAryExpr::getType().

Referenced by EvaluateConstantChrecAtConstant(), and llvm::SCEVApplyRewriter::visitAddRecExpr().

const Loop* llvm::SCEVAddRecExpr::getLoop ( ) const

inline

Definition at line 294 of file ScalarEvolutionExpressions.h.

Referenced by CollectSubexprs(), delinearize(), findIVOperand(), FindLoopCounter(), genLoopLimit(), llvm::ScalarEvolution::getAddExpr(), llvm::ScalarEvolution::getMulExpr(), getNumIterationsInRange(), getPreStartForSignExtend(), getStepRecurrence(), isExistingPhi(), isSimpleIVUser(), isStridedPtr(), llvm::SCEV::print(), llvm::SCEVParameterRewriter::visitAddRecExpr(), and llvm::SCEVApplyRewriter::visitAddRecExpr().

const SCEV * SCEVAddRecExpr::getNumIterationsInRange	(	ConstantRange	Range,
		ScalarEvolution &	SE
	)		const

getNumIterationsInRange - Return the number of iterations of this loop that produce values in the specified constant range. Another way of looking at this is that it returns the first iteration number where the value is not in the condition, thus computing the exit count. If the iteration count can't be computed, an instance of SCEVCouldNotCompute is returned.

Definition at line 6559 of file ScalarEvolution.cpp.

References llvm::ARM_PROC::A, llvm::ConstantRange::contains(), llvm::dyn_cast(), EvaluateConstantChrecAtConstant(), llvm::SCEV::FlagAnyWrap, llvm::SCEV::FlagNW, llvm::ConstantInt::get(), llvm::ScalarEvolution::getAddRecExpr(), llvm::ScalarEvolution::getConstant(), llvm::ScalarEvolution::getContext(), llvm::ScalarEvolution::getCouldNotCompute(), llvm::ConstantExpr::getICmp(), getLoop(), llvm::ConstantRange::getLower(), llvm::ScalarEvolution::getNegativeSCEV(), llvm::SCEVNAryExpr::getNoWrapFlags(), llvm::SCEVNAryExpr::getNumOperands(), llvm::SCEVNAryExpr::getOperand(), getStart(), llvm::SCEVNAryExpr::getType(), llvm::ScalarEvolution::getTypeSizeInBits(), llvm::ConstantRange::getUpper(), llvm::SCEVConstant::getValue(), llvm::ConstantInt::getValue(), llvm::CmpInst::ICMP_ULT, isAffine(), llvm::ConstantRange::isFullSet(), isQuadratic(), llvm::SCEVNAryExpr::op_begin(), llvm::SCEVNAryExpr::op_end(), llvm::SCEVNAryExpr::Operands, llvm::PPCISD::SC, llvm::APInt::sge(), SolveQuadraticEquation(), llvm::ConstantRange::subtract(), std::swap(), and llvm::APIntOps::udiv().

const SCEVAddRecExpr* llvm::SCEVAddRecExpr::getPostIncExpr ( ScalarEvolution & SE ) const

inline

getPostIncExpr - Return an expression representing the value of this expression one iteration of the loop ahead.

Definition at line 346 of file ScalarEvolutionExpressions.h.

References llvm::ScalarEvolution::getAddExpr(), and getStepRecurrence().

const SCEV* llvm::SCEVAddRecExpr::getStart ( ) const

inline

Definition at line 293 of file ScalarEvolutionExpressions.h.

References llvm::SCEVNAryExpr::Operands.

Referenced by CollectSubexprs(), delinearize(), evaluateAtIteration(), FindLoopCounter(), genLoopLimit(), llvm::ScalarEvolution::getAddExpr(), getNumIterationsInRange(), getPreStartForSignExtend(), and getSignExtendAddRecStart().

const SCEV* llvm::SCEVAddRecExpr::getStepRecurrence ( ScalarEvolution & SE ) const

inline

getStepRecurrence - This method constructs and returns the recurrence indicating how much this expression steps by. If this is a polynomial of degree N, it returns a chrec of degree N-1. We cannot determine whether the step recurrence has self-wraparound.

Definition at line 300 of file ScalarEvolutionExpressions.h.

References llvm::SCEV::FlagAnyWrap, llvm::ScalarEvolution::getAddRecExpr(), getLoop(), llvm::SCEVNAryExpr::getOperand(), isAffine(), llvm::SCEVNAryExpr::op_begin(), and llvm::SCEVNAryExpr::op_end().

Referenced by CollectSubexprs(), delinearize(), FindLoopCounter(), genLoopLimit(), getPostIncExpr(), getPreStartForSignExtend(), getSignExtendAddRecStart(), isLikelyComplexAddressComputation(), and isStridedPtr().

bool llvm::SCEVAddRecExpr::isAffine ( ) const

inline

isAffine - Return true if this is an affine AddRec (i.e., it represents an expressions A+B*x where A and B are loop invariant values.

Definition at line 309 of file ScalarEvolutionExpressions.h.

References llvm::SCEVNAryExpr::getNumOperands().

Referenced by delinearize(), FindLoopCounter(), genLoopLimit(), getNumIterationsInRange(), getStepRecurrence(), and hasComputableBounds().

bool llvm::SCEVAddRecExpr::isQuadratic ( ) const

inline

isQuadratic - Return true if this is an quadratic AddRec (i.e., it represents an expressions A+B*x+C*x^2 where A, B and C are loop invariant values. This corresponds to an addrec of the form {L,+,M,+,N}

Definition at line 318 of file ScalarEvolutionExpressions.h.

References llvm::SCEVNAryExpr::getNumOperands().

Referenced by getNumIterationsInRange().

void llvm::SCEVAddRecExpr::setNoWrapFlags ( NoWrapFlags Flags )

inline

Set flags for a recurrence without clearing any previously set flags. For AddRec, either NUW or NSW implies NW. Keep track of this fact here to make it easier to propagate flags.

Definition at line 325 of file ScalarEvolutionExpressions.h.

References llvm::SCEV::FlagNSW, llvm::SCEV::FlagNUW, llvm::SCEV::FlagNW, llvm::ScalarEvolution::setFlags(), and llvm::SCEV::SubclassData.

Referenced by llvm::ScalarEvolution::getAddRecExpr().

Friends And Related Function Documentation

friend class ScalarEvolution

friend

Definition at line 284 of file ScalarEvolutionExpressions.h.

The documentation for this class was generated from the following files:

Public Member Functions

Static Public Member Functions

Friends

Additional Inherited Members

Detailed Description

Member Function Documentation

Friends And Related Function Documentation