Extrusion {
eventIn MFVec2f set_crossSection
eventIn MFRotation set_orientation
eventIn MFVec2f set_scale
eventIn MFVec3f set_spine
field SFBool beginCap TRUE
field SFBool ccw TRUE
field SFBool convex TRUE
field SFFloat creaseAngle 0 # [0,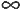 )
field MFVec2f crossSection [ 1 1, 1 -1, -1 -1,
-1 1, 1 1 ] # (-
)
field MFVec2f crossSection [ 1 1, 1 -1, -1 -1,
-1 1, 1 1 ] # (-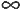 ,
,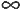 )
field SFBool endCap TRUE
field MFRotation orientation 0 0 1 0 # [-1,1],(-
)
field SFBool endCap TRUE
field MFRotation orientation 0 0 1 0 # [-1,1],(-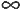 ,
,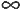 )
field MFVec2f scale 1 1 # (0,
)
field MFVec2f scale 1 1 # (0,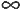 )
field SFBool solid TRUE
field MFVec3f spine [ 0 0 0, 0 1 0 ] # (-
)
field SFBool solid TRUE
field MFVec3f spine [ 0 0 0, 0 1 0 ] # (-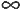 ,
,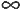 )
}
)
}
3.18.1 Introduction
The Extrusion node specifies geometric shapes based on a two dimensional
cross-section extruded along a three dimensional spine in the local
coordinate system. The cross-section can be scaled and rotated at each
spine point to produce a wide variety of shapes.
An Extrusion node is defined by:
- a 2D crossSection piecewise linear curve (described as a
series of connected vertices)
- a 3D spine piecewise linear curve (also described as a series
of connected vertices)
- a list of 2D scale parameters
- a list of 3D orientation parameters
3.18.2 Algorithmic description
Shapes are constructed as follows. The cross-section curve, which
starts as a curve in the Y=0 plane, is first scaled about the origin
by the first scale parameter (first value scales in X, second
value scales in Z). It is then translated by the first spine point and
oriented using the first orientation parameter (as explained
later). The same procedure is followed to place a cross-section at the
second spine point, using the second scale and orientation values. Corresponding
vertices of the first and second cross-sections are then connected,
forming a quadrilateral polygon between each pair of vertices. This
same procedure is then repeated for the rest of the spine points, resulting
in a surface extrusion along the spine.
The final orientation of each cross-section is computed by first orienting
it relative to the spine segments on either side of point at which the
cross-section is placed. This is known as the spine-aligned cross-section
plane (SCP), and is designed to provide a smooth transition from
one spine segment to the next (see Figure 3-21). The SCP is then rotated
by the corresponding orientation value. This rotation is performed
relative to the SCP. For example, to impart twist in the cross-section,
a rotation about the Y-axis (0 1 0) would be used. Other orientations
are valid and rotate the cross-section out of the SCP.
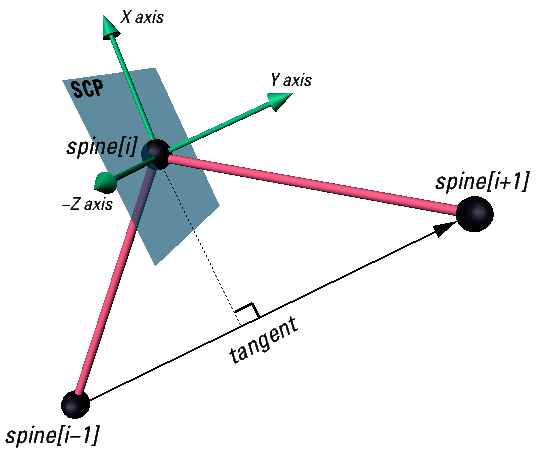
Figure 3-21: Spine-aligned cross-section plane at
a spine point.
The SCP is computed by first computing its Y-axis and Z-axis, then
taking the cross product of these to determine the X-axis. These three
axes are then used to determine the rotation value needed to rotate
the Y=0 plane to the SCP. This results in a plane that is the approximate
tangent of the spine at each point, as shown in Figure 3-21. First the
Y-axis is determined, as follows:
- For all points other than the first or last: The Y-axis
for spine[i] is found by normalizing the vector defined by
(spine[i+1] - spine[i-1]).
- If the spine curve is closed: The SCP for the first and
last points is the same and is found using (spine[1] - spine[n-2])
to compute the Y-axis.
- If the spine curve is not closed: The Y-axis used for the
first point is the vector from spine[0] to spine[1],
and for the last it is the vector from spine[n-2] to
spine[n-1].
The Z-axis is determined as follows:
- For all points other than the first or last: Take the following
cross-product:
Z = (spine[i+1] - spine[i]) X (spine[i-1] - spine[i])
- If the spine curve is closed: The SCP for the first and
last points is the same and is found by taking the following cross-product:
Z = (spine[1] - spine[0]) X (spine[n-2] - spine[0])
- If the spine curve is not closed: The Z-axis used for the
first spine point is the same as the Z-axis for spine[1]. The Z-axis
used for the last spine point is the same as the Z-axis for spine[n-2].
- After determining the Z-axis, its dot product with the Z-axis of
the previous spine point is computed. If this value is negative, the
Z-axis is flipped (multiplied by -1). In most cases, this prevents
small changes in the spine segment angles from flipping the cross-section
180 degrees.
Once the Y- and Z-axes have been computed, the X-axis can be calculated
as their cross-product.
3.18.3 Special cases
If the number of scale or orientation values is greater
than the number of spine points, the excess values are ignored. If they
contain one value, it is applied at all spine points. If the number
of scale or orientation values is greater than one but less than the
number of spine points, the results are undefined. The scale
values shall be positive.
If the three points used in computing the Z-axis are collinear, the
cross-product is zero so the value from the previous point is used instead.
If the Z-axis of the first point is undefined (because the spine is
not closed and the first two spine segments are collinear) then the
Z-axis for the first spine point with a defined Z-axis is used.
If the entire spine is collinear, the SCP is computed by finding the
rotation of a vector along the positive Y-axis (v1) to the
vector formed by the spine points (v2). The Y=0 plane is then
rotated by this value.
If two points are coincident, they both have the same SCP. If each
point has a different orientation value, then the surface is constructed
by connecting edges of the cross-sections as normal. This is useful
in creating revolved surfaces.
Note: combining coincident and non-coincident spine segments, as
well as other combinations, can lead to interpenetrating surfaces which
the extrusion algorithm makes no attempt to avoid.
3.18.4 Common cases
The following common cases are among the effects which are supported
by the Extrusion node:
- Surfaces of revolution:
- If the cross-section is an approximation of a circle and the spine
is straight, the Extrusion is equivalent to a surface of revolution,
where the scale parameters define the size of the cross-section
along the spine.
- Uniform extrusions:
- If the scale is (1, 1) and the spine is straight, the cross-section
is extruded uniformly without twisting or scaling along the spine.
The result is a cylindrical shape with a uniform cross section.
- Bend/twist/taper objects:
- These shapes are the result of using all fields. The spine curve
bends the extruded shape defined by the cross-section, the orientation
parameters (given as rotations about the Y-axis) twist it around the
spine, and the scale parameters taper it (by scaling about the spine).
3.18.5 Other fields
Extrusion has three parts: the sides, the beginCap (the
surface at the initial end of the spine) and the endCap (the
surface at the final end of the spine). The caps have an associated
SFBool field that indicates whether each exists (TRUE) or doesn't exist
(FALSE).
When the beginCap or endCap fields are specified as
TRUE, planar cap surfaces will be generated regardless of whether the
crossSection is a closed curve. If crossSection is not
a closed curve, the caps are generated by adding a final point to crossSection
that is equal to the initial point. An open surface can still have a
cap, resulting (for a simple case) in a shape analogous to a soda can
sliced in half vertically. These surfaces are generated even if spine
is also a closed curve. If a field value is FALSE, the corresponding
cap is not generated.
Texture coordinates are automatically generated by Extrusion nodes.
Textures are mapped so that the coordinates range in the U direction
from 0 to 1 along the crossSection curve (with 0 corresponding
to the first point in crossSection and 1 to the last) and in
the V direction from 0 to 1 along the spine curve (with 0 corresponding
to the first listed spine point and 1 to the last). If either
the endCap or beginCap exists, the crossSection
curve is uniformly scaled and translated so that the larger dimension
of the cross-section (X or Z) produces texture coordinates that range
from 0.0 to 1.0. The beginCap and endCap textures' S and
T directions correspond to the X and Z directions in which the crossSection
coordinates are defined.
The browser shall automatically generate normals for the Extrusion
node,using the creaseAngle field to determine if and how normals
are smoothed across the surface. Normals for the caps are generated
along the Y-axis of the SCP, with the ordering determined by viewing
the cross-section from above (looking along the negative Y-axis of the
SCP). By default, a beginCap with a counterclockwise ordering
shall have a normal along the negative Y-axis. An endCap with
a counterclockwise ordering shall have a normal along the positive Y-axis.
Each quadrilateral making up the sides of the extrusion are ordered
from the bottom cross-section (the one at the earlier spine point) to
the top. So, one quadrilateral has the points:
spine[0](crossSection[0], crossSection[1])
spine[1](crossSection[1], crossSection[0])
in that order. By default, normals for the sides are generated as
described in "2.6.3 Shapes and geometry."
For instance, a circular crossSection with counter-clockwise ordering
and the default spine form a cylinder. With solid TRUE and ccw
TRUE, the cylinder is visible from the outside. Changing ccw
to FALSE makes it visible from the inside.
The ccw, solid, convex, and creaseAngle
fields are described in "2.6.3 Shapes and
geometry."

