|
Chapter 3:
Node Reference
Intro
Anchor
Appearance
AudioClip
Background
Billboard
Box
Collision
Color
ColorInterpolator
Cone
Coordinate
CoordinateInterpolator
Cylinder
CylinderSensor
DirectionalLight
ElevationGrid
Extrusion
Fog
FontStyle
Group
ImageTexture
IndexedFaceSet
IndexedLineSet
Inline
LOD
Material
MovieTexture
NavigationInfo
Normal
NormalInterpolator
OrientationInterpolator
PixelTexture
PlaneSensor
PointLight
PointSet
PositionInterpolator
ProximitySensor
ScalarInterpolator
Script
Shape
Sound
Sphere
SphereSensor
SpotLight
Switch
Text
TextureCoordinate
TextureTransform
TimeSensor
TouchSensor
Transform
Viewpoint
VisibilitySensor
WorldInfo
|
Transform {
eventIn MFNode addChildren
eventIn MFNode removeChildren
exposedField SFVec3f center 0 0 0 # (-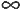 , ,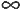 )
exposedField MFNode children []
exposedField SFRotation rotation 0 0 1 0 # [-1,1],(- )
exposedField MFNode children []
exposedField SFRotation rotation 0 0 1 0 # [-1,1],(-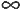 , ,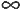 )
exposedField SFVec3f scale 1 1 1 # (0, )
exposedField SFVec3f scale 1 1 1 # (0,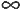 )
exposedField SFRotation scaleOrientation 0 0 1 0 # [-1,1],(- )
exposedField SFRotation scaleOrientation 0 0 1 0 # [-1,1],(-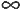 , ,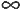 )
exposedField SFVec3f translation 0 0 0 # (- )
exposedField SFVec3f translation 0 0 0 # (-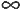 , ,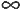 )
field SFVec3f bboxCenter 0 0 0 # (- )
field SFVec3f bboxCenter 0 0 0 # (-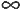 , ,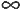 )
field SFVec3f bboxSize -1 -1 -1# (0, )
field SFVec3f bboxSize -1 -1 -1# (0,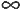 )
# or -1,-1,-1
} )
# or -1,-1,-1
}
The Transform node is a grouping node that defines a coordinate system
for its children that is relative to the coordinate systems of its ancestors.
See sections "2.4.4 Transformation hierarchy"
and "2.4.5 Standard units and coordinate
system" for a description of coordinate systems and transformations.
"2.6.5 Grouping and children nodes"
provides a description of the children, addChildren, and
removeChildren fields and eventIns.
The bboxCenter and bboxSize fields specify a bounding
box that encloses the children of the Transform node. This is a hint
that may be used for optimization purposes. If the specified bounding
box is smaller than the actual bounding box of the children at any time,
the results are undefined. A default bboxSize value, (-1, -1, -1),
implies that the bounding box is not specified and, if needed, must
be calculated by the browser. A description of the bboxCenter
and bboxSize fields is provided in "2.6.4
Bounding boxes."
The translation, rotation, scale, scaleOrientation
and center fields define a geometric 3D transformation consisting
of (in order):
- a (possibly) non-uniform scale about an arbitrary point
- a rotation about an arbitrary point and axis
- a translation
The center field specifies a translation offset from the origin
of the local coordinate system (0,0,0). The rotation field specifies
a rotation of the coordinate system. The scale field specifies
a non-uniform scale of the coordinate system. scale values shall
be > 0.0. The scaleOrientation specifies a rotation of
the coordinate system before the scale (to specify scales in arbitrary
orientations). The scaleOrientation applies only to the scale
operation. The translation field specifies a translation to the
coordinate system.
|
TIP:
The translation/rotation/scale operations performed by the Transform
node occur in the "natural" order—each operation is independent
of the other. For example, if the Transform's translation
field is (1, 0, 0), then the objects underneath the Transform
will be translated one unit to the right, regardless of the Transform's
rotation and scale fields. If you want to apply
a series of translate/rotate/scale operations in some other order,
you can either use nested Transform nodes or figure out the combined
transformation and express that as a single Transform node. As
long as all of your scaling operations are uniform scales (scale
equally about x-, y-, z-axes), then any series of scale/rotate/translate
operations can be expressed as a single Transform node.
Note
that negative scale values are not allowed, so the common trick
of defining one-half of an object and then mirroring it (using
a negative scale and USE-ing the geometry again) will not work.
Interactive programs will still provide mirroring operations,
of course, but when saving to a VRML file the program will have
to duplicate the mirrored polygons to avoid the negative scale.
|
Given a 3-dimensional point P and Transform node, P
is transformed into point P' in its parent's coordinate system
by a series of intermediate transformations. In matrix transformation
notation, where C (center), SR (scaleOrientation), T (translation),
R (rotation), and S (scale) are the equivalent transformation
matrices,
P' = T × C × R × SR × S × -SR × -C × P
The following Transform node:
Transform {
center C
rotation R
scale S
scaleOrientation SR
translation T
children [...]
}
is equivalent to the nested sequence of:
Transform {
translation T
children Transform {
translation C
children Transform {
rotation R
children Transform {
rotation SR
children Transform {
scale S
children Transform {
rotation -SR
children Transform {
translation -C
children [...]
}}}}}}}
TECHNICAL
NOTE: VRML
1.0 included special-purpose versions of Transform—Scale, Rotate,
and Translate nodes—and the more general MatrixTransform node.
The special-purpose nodes were dropped from VRML 2.0 because they
are equivalent to a Transform node with some of its fields left
as default values. If their absence bothers you, their prototype
definitions are trivial. For example:
PROTO Translate [ exposedField SFVec3f translation ] {
Transform { translation IS translation }
}
Dropping
MatrixTransform was much more controversial. Allowing arbitrary
matrix transformations was a very powerful feature that is almost
impossible to support in its full generality. The arbitrary 4×4
matrix of the MatrixTransform allows specification of perspective
transformations that have singularities and degenerate matrices
that cannot be inverted, both of which cause major implementation
headaches. Lighting operations, for example, typically rely on
transforming normal vectors by the inverse transpose of the transformation
matrix, which is a big problem if the matrix cannot be inverted.
And picking operations (determining which geometry is underneath
the pointing device) are best done by transforming a picking ray
into the object's coordinate space, which, again, is impossible
if there is a degenerate or perspective transformation in the
transformation stack. No VRML 1.0 browser completely implements
the MatrixTransform node.
Restricting
the legal values of a MatrixTransform was suggested, but doing
that makes MatrixTransform just another representation for the
Transform node. Since that representation is both more verbose
(16 numbers, four of which would always be (0, 0, 0, 1) versus
the ten for a simple translate/rotate/scale Transform node), conversion
back and forth between the two representations is possible (see
the Graphics Gems series of books by Academic Press for several
approaches). MatrixTransform was used in relatively few VRML 1.0
worlds, and one of the design goals for VRML 2.0 was minimalism.
For all of these reasons, MatrixTransform is not part of the VRML
2.0 specification.
|
TIP:
To
use the Transform node properly, it is important to understand
the order of the transformation operations as they accumulate.
The first step is the center field. It translates the local
origin of the object to a new position before all the other operations
take place. It does not translate the object and will have no
effect if no other operations are specified. Think of this operation
as specifying the location of the object's center point to be
used for subsequent operations (e.g., rotation). For example,
the default Box node is centered at (0,0,0), and represents a
cube that spans -1 to +1 along all three axes. In the following
file excerpt, the Box is parented by a Transform that specifies
a center of (-3,0,0) and a rotation of +180 degrees about the
Z-axis of the modified center. The result is an upside-down box
centered at (-6,0,0):
Transform {
center -3 0 0
rotation 0 0 1 3.14
children Shape { geometry Box {} }
}
The second
operation, in order, is the scaleOrientation. This operation
is the most obscure and is rarely used. The scaleOrientation
temporarily rotates the object's coordinate system (i.e., local
origin) in preparation for the third operation, scale, and rotates
back after the scale is performed. This is sometimes handy when
you wish to scale your object along a direction that is not
aligned with the object's local coordinate system (e.g., skewing).
The fourth operation is rotation. It specifies an axis
about which to rotate the object and the angle (in radians)
to rotate. Remember that positive rotations produce counterclockwise
rotations when viewed down the positive axis. This is sometimes
referred to as the right-hand rule (see any computer graphics
or VRML tutorial book for an explanation). The last operation
is translation. It specifies a translation to be applied
to the object. Remember that translation will occur along the
local axes of the object's coordinate-system.
|
TIP:
Another
important concept to understand is the order in which nested
Transforms operate. Within a single Transform the operation
order occurs as described, but when a Transform parents another
Transform, the lowest level Transform is applied first and each
subsequent parent's operations are applied in "upward" order.
For example, the following excerpt defines two Transforms, T1
and T2. The first Transform, T1, performs a translation and
a scale operation, and has a child T2. The Transform T2 performs
a scale and a rotation operation. Therefore, the order of operations
is: T2 scale, T2 rotation, T1 scale, and finally T1 translation.
It is important to notice that T1's scale operation scales the
rotated object (and produces a skew):
DEF T1 Transform {
scale 1 2 1 # Stretch along Y
translation 0 0 -3 # Translate back in Z
children DEF T2 Transform {
scale 1 1 10 # Stretch in Z
rotation 1 0 0 0.785 # Rotate 45 degrees, X axis
children Shape { geometry Box {} }
}
}
|
EXAMPLE
(click to run):
The following example illustrates the Transform node. The
first Transform, T1, is the parent transformation for all
subsequent objects in the file. The second Transform, T2,
uses default values and is transformed by its parent's transformations.
The third Transform, T3, specifies a new center point and
a rotation about that center point. Note that these operations
take place before the T1's scale and translation. The fourth
Transform, T4, scales and translates the object, and of course
is also transformed by T1.
#VRML V2.0 utf8
DEF T1 Transform { # Parent xform for entire file
translation 0 0 -100 # Xlates entire file down Z
scale 1 2 1 # Scales entire file in Y
children [
DEF T2 Transform { # Default transform at origin
children Shape {
geometry Box {}
appearance Appearance {
material Material { diffuseColor 1 0 0 }
}}}
DEF T3 Transform { # Re-centered and rotated
center -3 0 0
rotation 0 0 1 3.14
children Shape {
geometry Cone {}
appearance Appearance {
material Material { diffuseColor 0 1 0 }
}}}
DEF T4 Transform { # Scaled (half) and xlated +X
scale 0.5 0.5 0.5
translation 3 0 0
children Shape {
geometry Cylinder {}
appearance Appearance {
material Material { diffuseColor 0 0 1 }
}}}
]
}
|
|

